Year 10+ Plane Geometry
Chapters
Parabolas
Parabolas
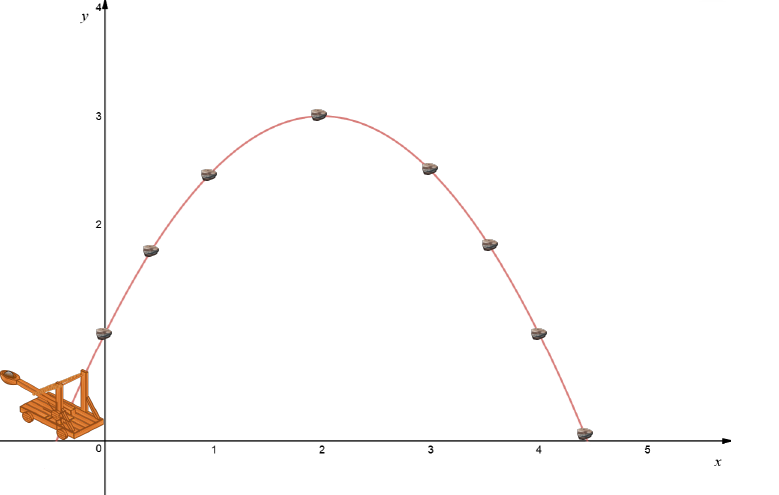
When you throw a cricket ball, shoot an arrow, kick a footy ball, fire a catapult, fire an arrow or hit a golf ball, it takes an arc-shaped
path through the air and comes down to land again some distance away from you. The path of your projectile is like a parabola, except that
air resistance modifies it a bit.
Telescopes and headlights use reflective lenses shaped like parabolas because special properties of the parabola focus all the light at one point.
So, what exactly is a parabola?
Definition of the Parabola
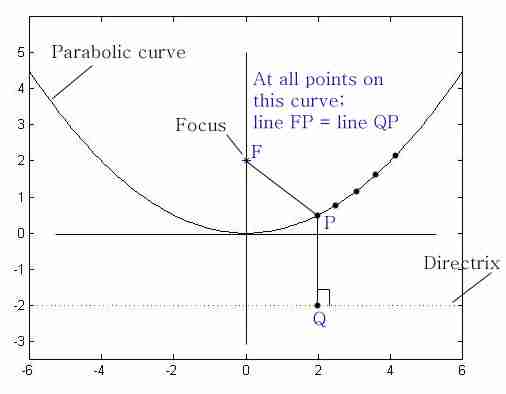
Formally, a parabola is the locus of a point that moves so that its distances from a fixed
point called the focus and a fixed line called the directrix are equal
The ratio between the distances of a point to the focus and the distances of a point to the directrix in a conic section is called the eccentricity, and it measures how far the conic
is from being a circle. In a parabola, the eccentricity is always equal to \(1\) because these distances are always equal.
Parts of a Parabola
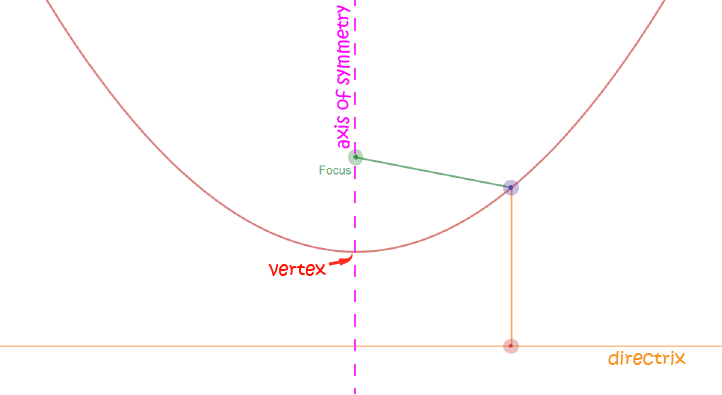
When you are doing problems on parabolas, it will help if you can name the important parts of a parabola. They are:
- The
directrixandfocus: the fixed line and fixed point talked about above. - The
axis of symmetry: a line through the focus at right angles to the directrix that cuts the parabola evenly in half. - The
vertex: the point where the parabola turns around and goes in the other direction. It is halfway between the focus and the directrix.
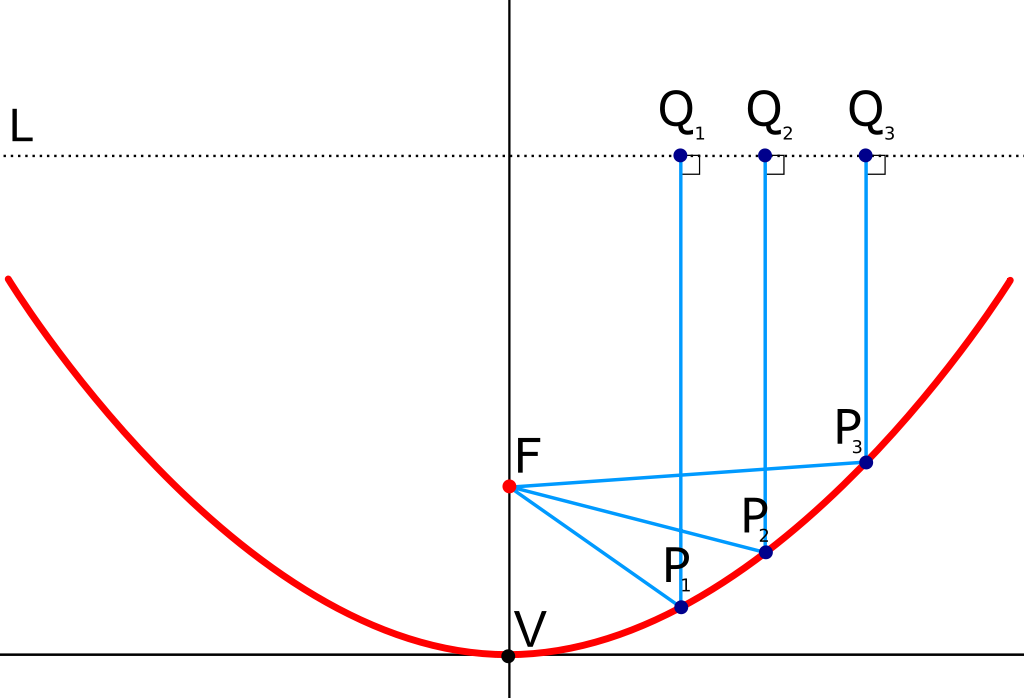
What Makes the Parabola so Useful in Torches and Telescopes?
The parabola has a special property that makes it a great shape to use in
- telescopes
- torches and spot lights
- radar dishes
- satellite dishes
- bananas (not really - but see later)
- solar collectors for solar panels

It's this:
If the inside of a parabola is hit by a ray that is parallel to the parabola's axis of symmetry, then the ray is reflected off the surface of the parabola, directly to the focus.
This helps to concentrate light, radio or digital signals for collection at the focus of the parabola.
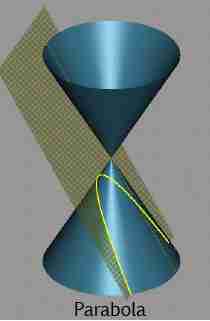
The Parabola as a Conic Section
A parabola appears as a cross-section of a cone, when you take a slice parallel to the cone's side.
Thus, the parabola is a conic section. You can read more about conic sections in the article on conic sections.
The Equation of a Parabola
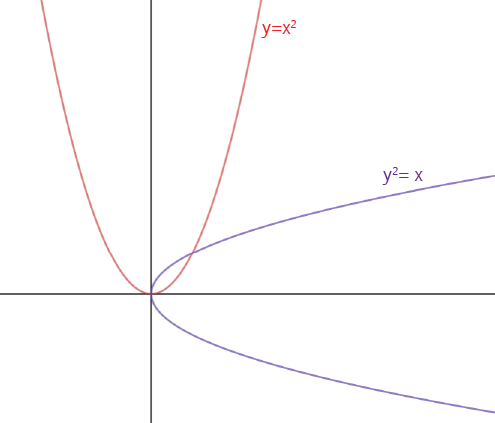
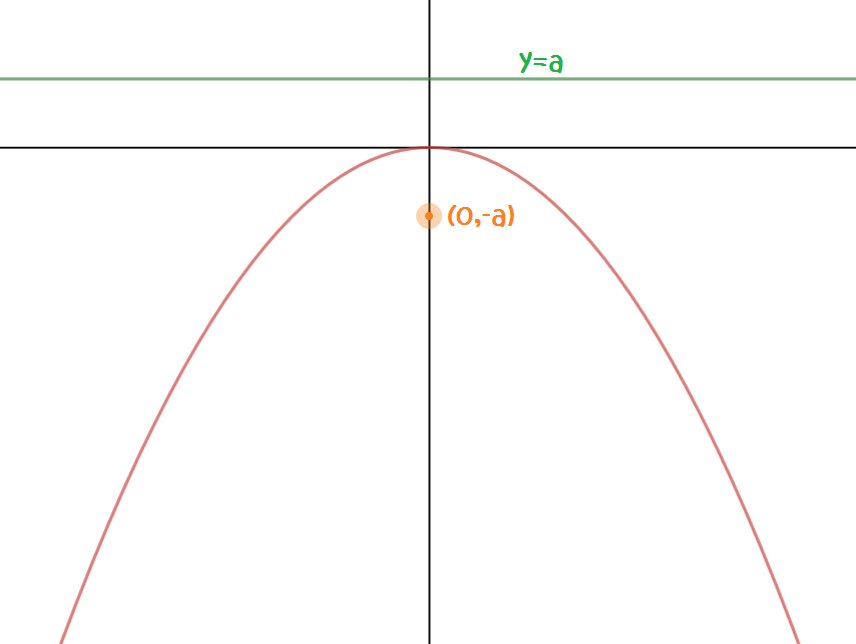
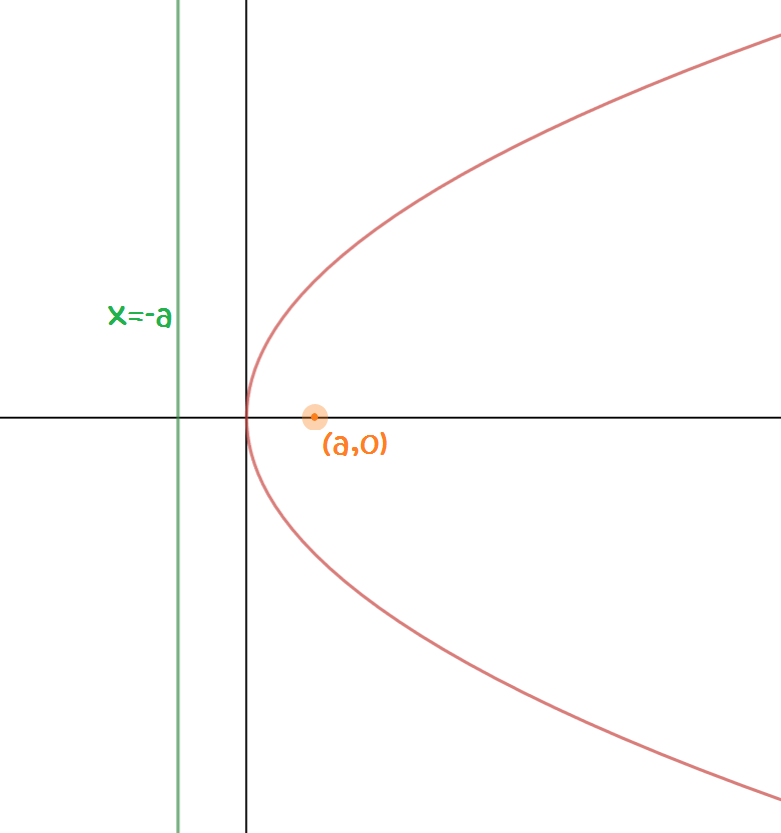
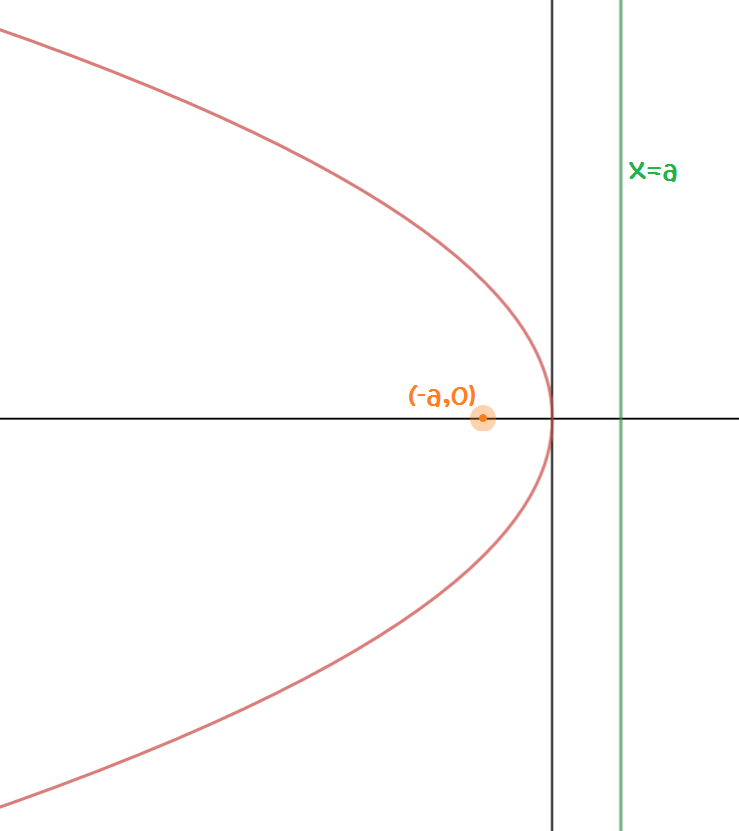
We can plot parabolas in the \(xy\)-plane. The simplest parabolas have their vertices at the origin, and either face upwards or to the side like these two graphs of \(y = x^2\) and \(y^2 = x\):
The general equation of a sideways parabola (opening to the right) with its vertex at the origin is
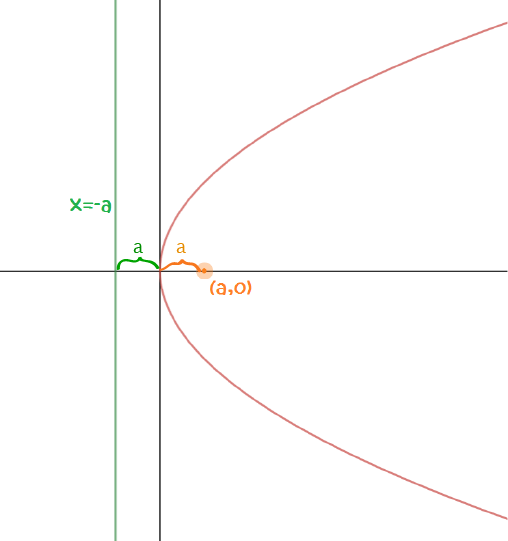
Here \(a\) is called the focal length. It is the distance from the vertex to the focus (and from the vertex to the directrix).
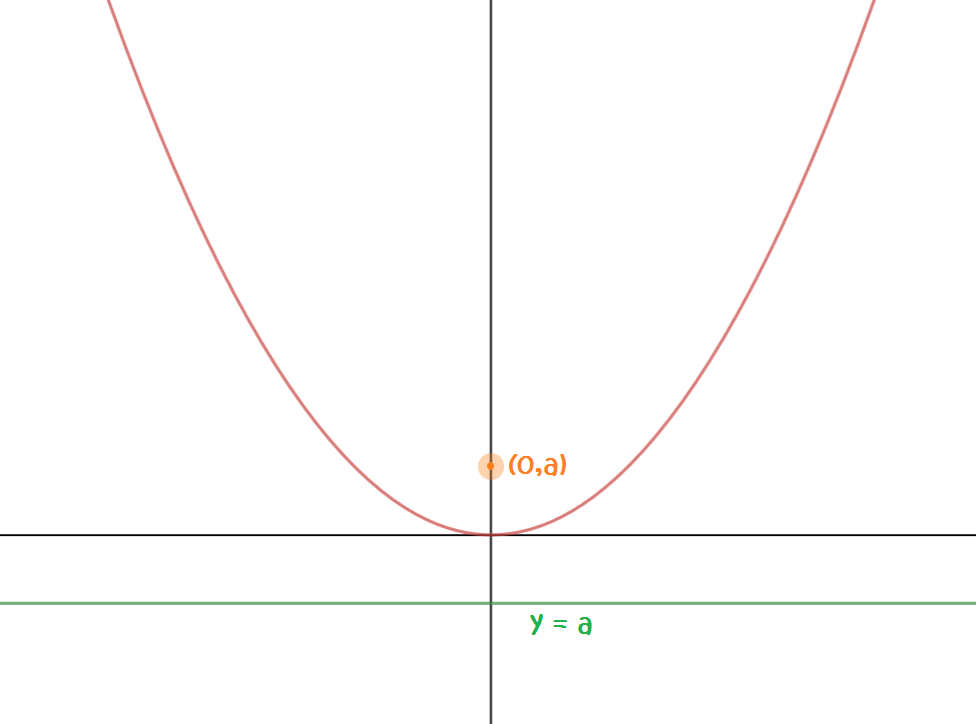
We can find equations for a parabola with vertex \((0,0)\) that opens upwards, downwards to the left and to the right as follows:
Examples
- Find the focus of the parabola \(32y = x^2\). Which way does the parabola face?
Solution:The focal length is \(a = 32 \div 4 = 8\). As the equation includes a term in \(x^2\) and the coefficient of \(y\) is positive, the parabola opens upwards. The focus is the point \((0,8)\).
- Find the focus of the parabola \(y^2 = 16 x\). Which way does the parabola face?
Solution:The focal length is \(a = 16 \div 4 = 4\). As the equation includes a term in \(y^2\) and the coefficient of \(x\) is positive, the parabola opens to the right. The focus is the point \((4,0)\).
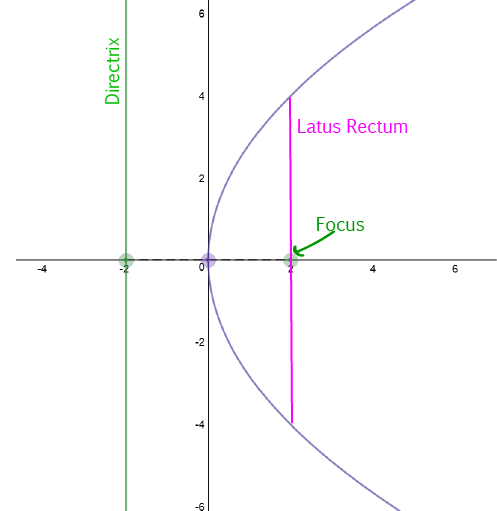
Latus Rectum of a Parabola
The latus rectum of a hyperbola is a line segment that runs through the focus of the parabola, parallel to the directrix.
Parabolas in Real Life

Parabolas occur in many situations, both naturally and in art and architecture.
The curve of the banana on the left is a parabola.
The view of the Sydney Harbour Bridge shown on the right includes two different parabolas. Can you find them? What would their equations look like?

Description
In these chapters you will learn about plane geometry topics such as
- Area (Irregular polygons, plane shapes etc)
- Perimeter
- Conic sections (Circle, Ellipse, Hyperbola etc)
- Polygons (Congruent, polygons, similar, triangles etc)
- Transformations and symmetry (Reflection, symmetry, transformations etc)
etc
Even though these chapters are marked for Year 10 or higher students, several topics are for students in Year 8 or higher
Audience
Year 10 or higher, suitable for Year 8 + students as well.
Learning Objectives
Learn about Plane Geometry
Author: Subject Coach
Added on: 28th Sep 2018
You must be logged in as Student to ask a Question.
None just yet!