Translations

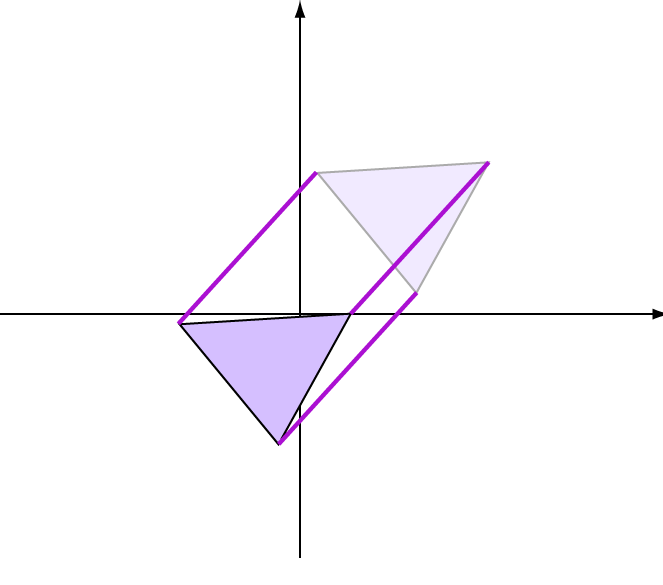
Translation is one of the most important geometrical transformations. Another term for translation is slide. In a translation, every point of an object is moved by the same amount in the same direction. So, translation does not change the lengths of the lines or the angles of the object.

There are two different ways you can specify a translation:

1. Specifying a distance and a direction (angle)
2. Using coordinates.

Specifying a distance and a direction

To draw a translated polygon in a specified distance and direction:

1. Draw line segments from each vertex of the specified length at the specified angle to horizontal (These will be parallel).
2. Join the ends of the line segments to form the translated shape.

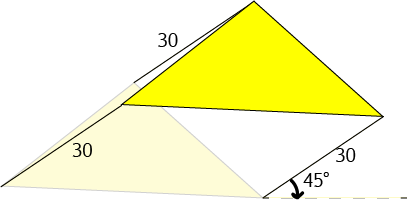
In this picture, every point of the triangle is translated by 30 units at an angle of \(45^\circ\) to the horizontal. The original shape is the paler yellow triangle.

Do you notice how the lengths of all the lines, and the angles between the pairs of lines remain the same?

Using Coordinates

You can also specify how much the object is to be translated in the \(x\) and \(y\)-directions using coordinates. For example, translating by \((15,20)\) means to move the object 15 units to the right, and then 20 units up.

The picture shows a triangle that has been translated 2 units to the right and 3 units up.

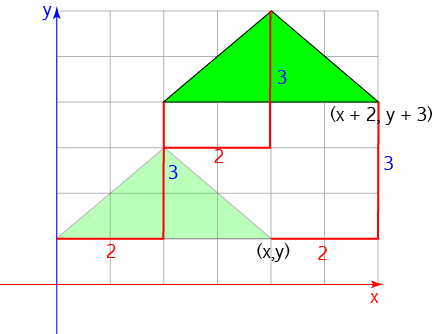
This has the same effect as turning each coordinate \((x,y)\) into \((x + 2, y + 3)\).

To draw a polygon that has been translated by coordinates \((a,b)\):

1. Draw a copy of each vertex a units to the right of the original vertex, and b units above it. (If a is negative, you will need to draw the vertex to the left, and if b is negative, you will need to draw the vertex further down the plane).
2. Join the new translated vertices with straight line segments to make a copy of the original polygon.

Now you have a translated polygon. Walk around with an incredibly smug expression on your face, telling yourself how clever you are.

You can use this technique to build yourself all sorts of geometric patterns like tessellations of the plane. Have fun!