Perimeter of an Ellipse

An ellipse is pretty simple to describe, isn't it? And its area is easy to calculate. It turns out, however, that it is incredibly difficult to calculate its perimeter.

The problem of finding formulas for the perimeter of an ellipse has fascinated mathematicians for centuries. In fact, I've just read a new paper in which the author claims to have come up with an elementary formula that gives an approximation for the perimeter of an ellipse that is very accurate. I'll tell you about it in a little while. There are some formulas that give you exact values for the perimeter of an ellipse, but they involve infinite series. We'll talk more about those later. First we need to size up our ellipse.

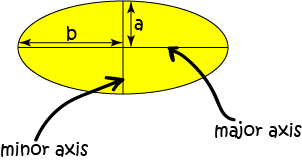
In the above picture, \(a\) is half the length of the major axis of the ellipse, and \(b\) is half the length of the minor axis of the ellipse. Think of them as radii: they are measured from the centre to the perimeter, and if they were equal, the ellipse would be a circle.

The Obvious Approximation

The circumference of a circle is equal to \(2 \pi r\), where \(r\) is the radius. So, you'd think that the perimeter of an ellipse would be equal to \(\pi(a + b)\). Unfortunately, this only works when the ellipse is almost a circle.

An Approximation that Works for Ellipses that are More Squashed.

So long as \(a\) is not greater than \(3\) times \(b\), the following approximation lies within about \(5\%\) of the true perimeter:

It actually gives an underestimate for the perimeter.

An overestimate for the perimeter is given by

Taking the average of these two will give a better approximation.

Ramanujan's Work

Srinivasa Ramanujan (1887-1920) was an Indian mathematician who published prolifically in many fields. It isn't surprising that he came up with a two different approximations to the perimeter of an ellipse that are better than either of the ones we've already looked at. These are:

1. \(P \approx \pi \left[3(a + b) - \sqrt{(3a + b)(a + 3b)}\right]\) and
2. If \(h = \dfrac{(a - b)^2}{(a + b)^2}\), then \(P \approx \pi(a + b) \left( 1 + \dfrac{3h}{10 + \sqrt{4 - 3h}}\right)\)

The New Approximation I Found

Today, I read a paper by a mathematician, Shahran Zafary, who claims that the following approximation is accurate to within \(0.17\%\) of the true perimeter:

It is exact when the ellipse is a circle (i.e. when \(a = b\)), and when the ellipse has degenerated into a pair of straight lines (i.e. when \(b = 0\)).

Formulas Using Infinite Series

These formulas are exact, but the problem is that you have to add up infinitely many terms to get the exact answer. Of course, we can never do that, so, in practice these just give approximations as well.

Series 1

First, find the eccentricity, \(e\), of the ellipse using the formula

Next, sum the series

This looks like a real mess, but the expansion gives

Unfortunately, you need to calculate a lot of terms of this series before you get an approximation that is close to the perimeter. Mathematicians say that this series converges (approaches the answer) slowly.

Series 2

This series gets close to the answer after only a few terms.

First, calculate

Next, sum the series

where \(\begin{pmatrix}0.5\\n \end{pmatrix}\) is a special kind of binomial coefficient. This looks pretty scary, but the expansion looks like this:

The additional terms get smaller very quickly, so we only need to calculate a few terms to find an accurate approximation to the perimeter of the ellipse.

Conclusion

There are many other approximations for the perimeter of an ellipse. A lot of them involve very complicated mathematics. I think it's probably better to opt for a piece of string and a ruler to measure the perimeter of your ellipse.