Year 10+ Plane Geometry
Chapters
Theorems About Circles
Theorems About Circles
This article talks about some interesting theorems that you will encounter when exploring the geometry of circles. Of course, there are many other theorems about circles. This just gives you an introduction.
Inscribed Angle Theorems
An inscribed angle is an angle that is formed by two chords to a circle that meet at a point. The point where they meet is the
apex of the angle.
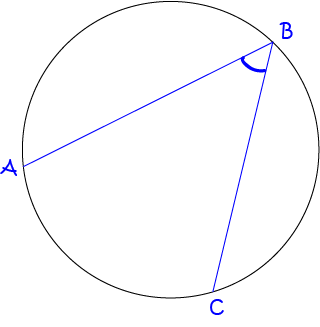
Theorem 1
The angle at the centre of the circle is twice the size of the inscribed angle standing on the same arc.
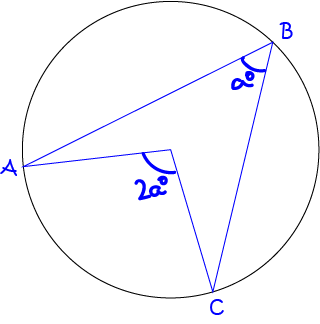
angle at the centre of a circle theorem.
Theorem 2
Angles at the circumference of a circle standing on the same arc are always equal.
In other words, two inscribed angles standing on the same arc are always equal.
This theorem is sometimes called the angles subtended by the same arc theorem.
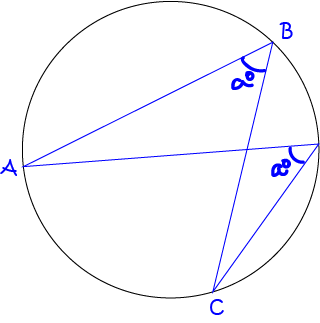
Example 1
Find the value of \(a^\circ\).
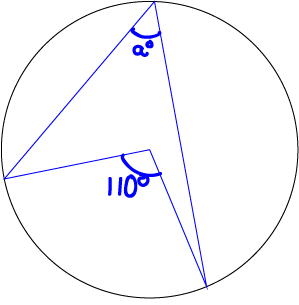
The angle marked with \(a^\circ\) is the angle at the circumference standing on the same arc as the angle marked with \(110^\circ\) at the centre of the circle.
Therefore, by Theorem 1,
Example 2
Find \(\angle ABX\) in the picture.
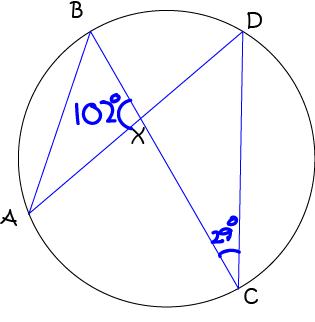
Angles \(AXB\) and \(CXD\) are vertically opposite, and therefore equal. Therefore, \(\angle CXD = 102^\circ\).
Now \(\angle CDX = 180^\circ - 102^\circ - 29^\circ = 49^\circ\) (angle sum of triangle \(CXD\)).
Finally, \(\angle ABX = \angle CDX = 49^\circ\) (angles at the circumference standing on the same arc).
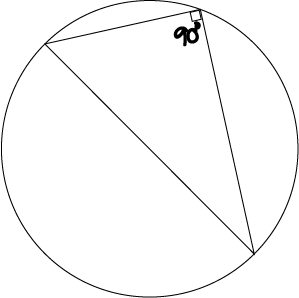
Angle in a Semicircle
Regardless of where it's drawn, the angle in a semicircle is always a right angle.
The end points of the angle in a semicircle are the ends of a diameter of the circle.
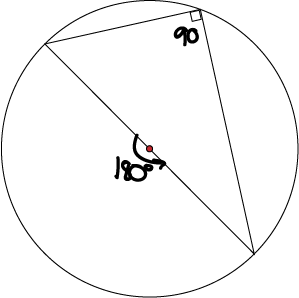
We can see this as a direct consequence of the angle at the centre of the circle theorem (Theorem 1 above). The angle at the centre of the circle in this case is \(180^\circ\) because the angle at the circumference is subtended by a diameter. Therefore, the angle at the circumference is half the central angle, or \(\dfrac{1}{2} (180^\circ) = 90^\circ\).
Example 3
Find \(\angle ABC\).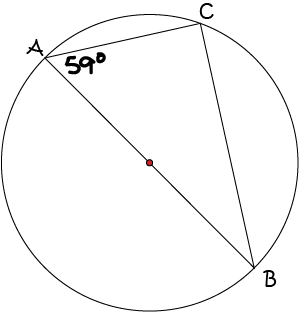
Now, \(\angle ACB\) is the angle in a semicircle, so \(\angle ACB = 90^\circ\).
\(\angle ABC\) is now the only unknown angle of the triangle \(ACB\). Since the angle sum of a triangle is \(180^\circ\),
Cyclic Quadrilaterals
A cyclic quadrilateral is a quadrilateral whose 4 vertices lie on the circumference of a circle.
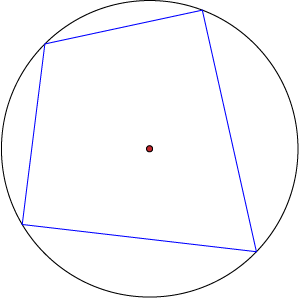
The opposite angles of a cyclic quadrilateral are supplementary (add up to \(180^\circ\)).
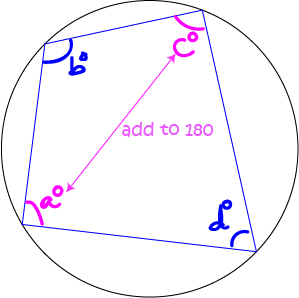
In the above picture,
- \(a + c = 180^\circ\) and
- \(b + d = 180^\circ\).
Example 4
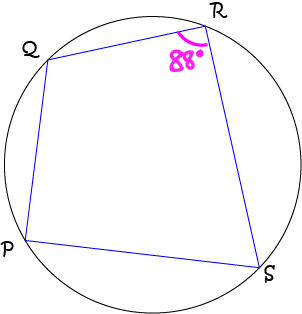
Find the size of \(\angle QPS\) in the picture.
Solution:
Since the opposite angles of a cyclic quadrilateral are supplementary,
Theorems About Tangents
A tangent is a line that touches a circle at a single point (called the point of contact).
There are many theorems about tangents to a circle. Here's one of them.
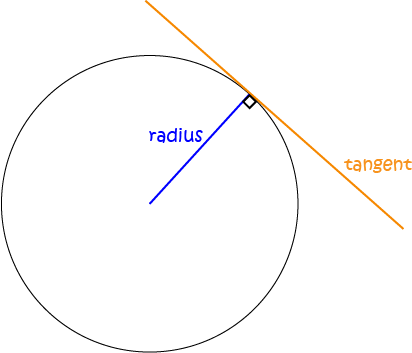
The tangent to a circle forms an angle of \(90^\circ\) with the radius at the point of contact.
As I said, this article only skims the surface of circle geometry. Many other theorems are known about circles, but most of them can be derive from the theorems in this article.
Do you want to find out more about circles? Have a read of the article on segments and sectors.
Description
In these chapters you will learn about plane geometry topics such as
- Area (Irregular polygons, plane shapes etc)
- Perimeter
- Conic sections (Circle, Ellipse, Hyperbola etc)
- Polygons (Congruent, polygons, similar, triangles etc)
- Transformations and symmetry (Reflection, symmetry, transformations etc)
etc
Even though these chapters are marked for Year 10 or higher students, several topics are for students in Year 8 or higher
Audience
Year 10 or higher, suitable for Year 8 + students as well.
Learning Objectives
Learn about Plane Geometry
Author: Subject Coach
Added on: 28th Sep 2018
You must be logged in as Student to ask a Question.
None just yet!