Hyperbolas

Did you know that, when satellites are launched into space, astronomers use hyperbolas to predict their paths so that they can make the adjustments that are necessary to ensure they get to their intended destinations?

Telescopes make use of hyperbolic lenses to increase their magnification within a confined space.

During World War II, scientists in the United States developed the LORAN system (short for long range navigation), which used hyperbolas to identify the positions of ships and aircraft near the United States coastline.

These are all practical uses of hyperbolas, but what exactly are they?

Definition of the Hyperbola

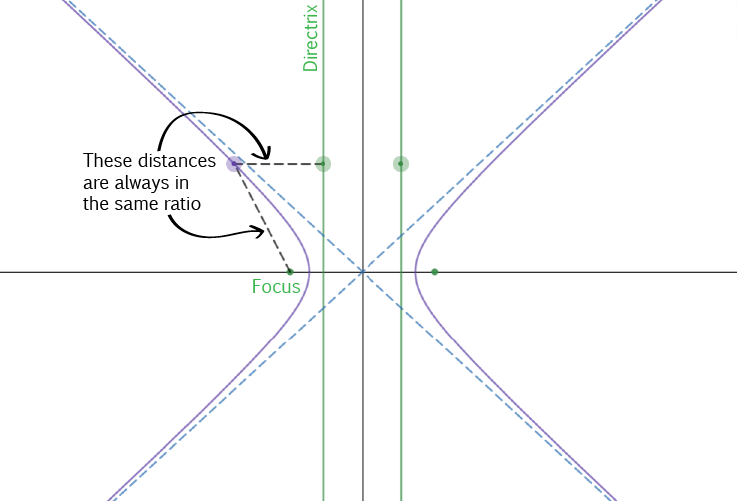
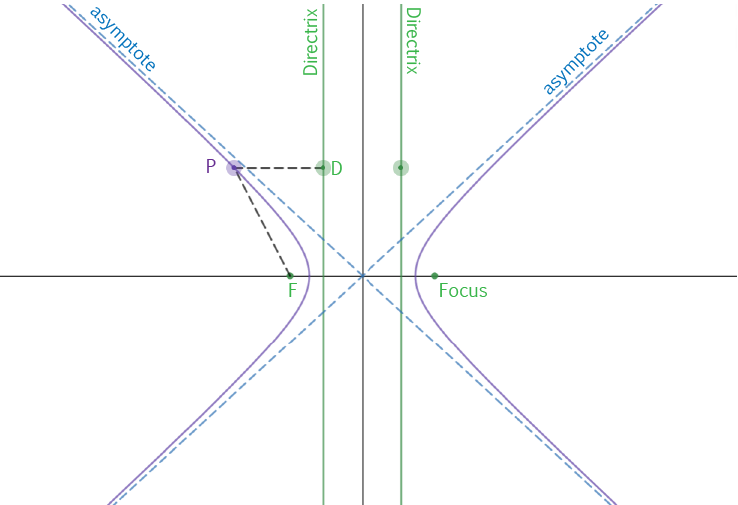
Formally, a hyperbola is the locus of a point that moves so that the ratio between its distances from a fixed point called the focus and a fixed line called the directrix is kept constant.

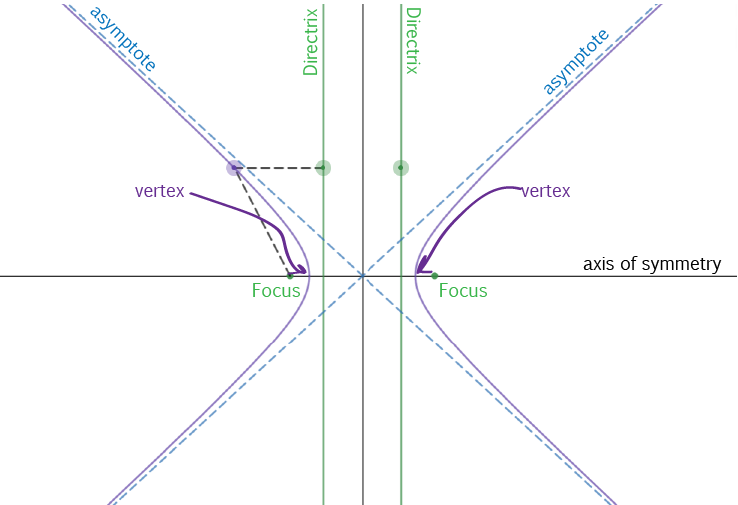
A hyperbola actually has two halves, so it has two foci (the plural of focus) and two directrices (the plural of directrix).

Each half is a reflection of the other half in an axis of reflection that passes through each focus (and in a line runs parallel to, and is equidistant from, the two directrices).

The vertices of the hyperbola are the points where it makes its sharpest turn. The hyperbola has two vertices: one on each half.

The ratio between the distance of a point to the focus and the distance of a point to the directrix is called the eccentricity, and it measures how far the conic is from being a circle. In a hyperbola, the eccentricity is always greater than \(1\).

The diagram also shows two lines called asymptotes: these are not strictly part of the hyperbola, but show the graph that the curve approaches for very large values of \(x\) and \(y\).

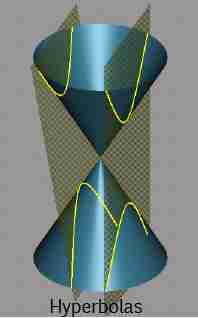
The Hyperbola as a Conic Section

A hyperbola appears as a cross-section of a cone, made at a steep angle. This slice does not have to be parallel to the cone's axis, but it must be very steep. Thus, the hyperbola is a conic section. You can read more about conic sections in the article on conic sections.

The Equation of a Hyperbola

We can plot hyperbolas in the \(xy\)-plane. If we put the centre of the hyperbola at the origin, its equation is:

The vertices of the hyperbola are at \((a,0)\) and \((-a,0)\).

The asymptotes of the hyperbola are \(y = \dfrac{b}{a}\;x\) and \(y = -\dfrac{b}{a}\;x\).

Here's the graph:

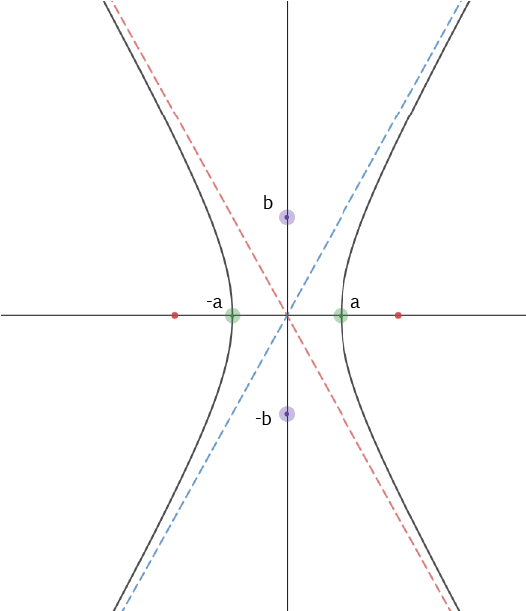
If you've read the article, or know about, ellipses, then you'll realise that this equation is similar to the equation of an ellipse. The difference is that the equation for ellipse has a plus in the middle.

Eccentricity of a Hyperbola

The eccentricity (symbol \(e\)) shows how much the hyperbola differs from being a circle.

It is equal to the ratio of the distance of a point \(P\) on the hyperbola from the focus \(F\) to the perpendicular distance between the point \(P\) and the directrix. In this diagram, it is equal to the ratio \(\dfrac{PF}{PD}\), which is always greater than \(1\).

If we know the equation of the hyperbola, we can find its eccentricity using the formula

\( e = \dfrac{\sqrt{a^2 + b^2}}{a}. \)

Latus Rectum of a Hyperbola

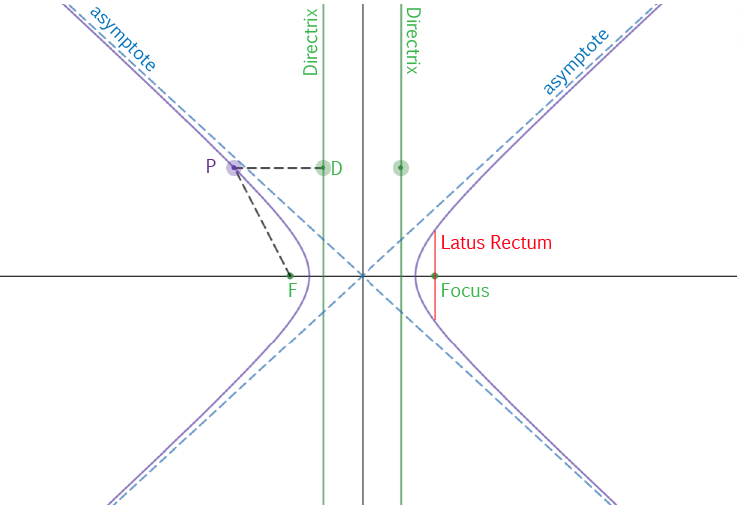
The latus rectum of a hyperbola is a line segment that runs through the focus of the hyperbola, parallel to the directrix. As the hyperbola has two foci, it has two latus recta (the plural of latus rectum).

If we know the equation of the hyperbola, we can find the length of its latus recta: \(\dfrac{2b^2}{a}\).