Year 10+ Coordinate Geometry
Chapters
The Square Function
The Square Function
The square function is the function
Here's a table of some values for the square function:
| \(x\) | \(f(x)\) |
|---|---|
| \(-3\) | \(9\) |
| \(-2\) | \(4\) |
| \(-1\) | \(1\) |
| \(0\) | \(0\) |
| \(0.5\) | \(0.25\) |
| \(1\) | \(1\) |
| \(2\) | \(4\) |
| \(3\) | \(9\) |
| \(\text{elephant}\) | \(\text{elephant}^2\) |
| \(\pi\) | \(\pi^2 \approx 9.8696\) |
And here's its graph:
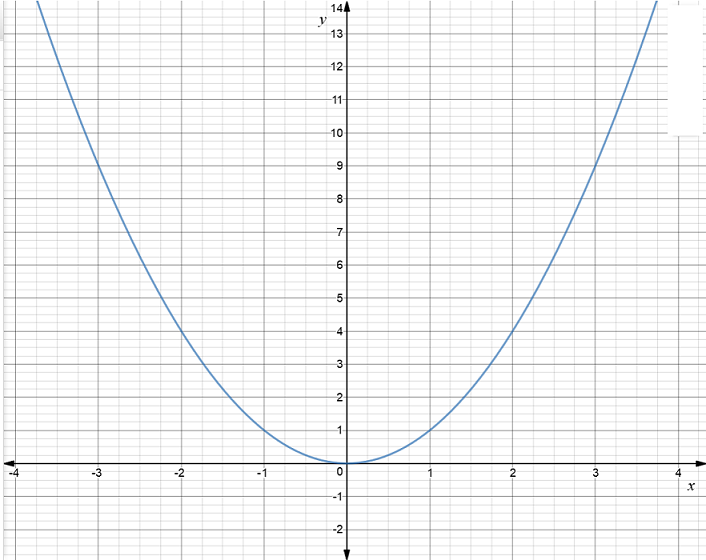
We call graphs with this shape parabolas.
Properties of the Square Function
Its domain is the set of all real numbers.
Its range is the set of non-negative real numbers: \([0,\infty)\).
Its minimum value is at \((0,0)\). We call this the vertex of the parabola. This is the point where the parbola turns around.
It has no maximum value.
It is increasing for \(x > 0\) and decreasing for \(x
It is symmetric about the \(y\)-axis. If you stick a mirror along the \(y\)-axis, one half of the square function will reflect exactly onto the other half.
It is an even function: \(f(x) = f(-x)\) for all real \(x\).
Description
A coordinate geometry is a branch of geometry where the position of the points on the plane is defined with the help of an ordered pair of numbers also known as coordinates. In this tutorial series, you will learn about vast range of topics such as Cartesian Coordinates, Midpoint of a Line Segment etc
Audience
year 10 or higher, several chapters suitable for Year 8+ students.
Learning Objectives
Explore topics related to Coordinates Geometry
Author: Subject Coach
Added on: 27th Sep 2018
You must be logged in as Student to ask a Question.
None just yet!