Solving Systems of Linear Equations: Substitution

Gus and Alyce

Let's see if we can use algebra to sort out the situation with Gus and Alyce. We'll start with question 1. We have the system of linear equations:

Both of these equations start with \(y = \text{something}\), so the easiest thing to do is to set them both equal to each other like this:

Subtracting \(3x\) from both sides yields which is just plain false, so the system has no solution (it is inconsistent) and the snails won't crash.

How about question 2? This time we have the system of linear equations:

If we set them both equal to each other like this:

then adding \(3\) to both sides yields and subtracting \(2x\) from both sides gives Now plug this into one of the equations to find \(y\): So, the solution is \(x = 4\) and \(y = 9\). The snails collide at the point \((4,9)\).

Subsitution

Sometimes systems of equations aren't set up as nicely as in the Gus and Alyce example, and we have to be a bit trickier when we're trying to solve them. There are two commonly used techniques for solving systems of linear equations: substitution and elimination. We're going to look at solving systems by substitution here. We'll deal with elimination in another article.

There are a number of steps involved in solving systems of linear equations by substitution (the number of times you repeat them depends on the number of variables in your system). Here they are:

1. Make one variable the subject of one of the equations (e.g. \(y = 3x - 4\)).
2. Replace (substitute) that variable with the expression on the right hand side of the expression from step 1.
3. Solve the other equation(s).
4. You may need to repeat this process for other variables if your system has more than two variables as your solution will be given in terms of some of the other variables.
5. Check your solution satisfies all of the equations.

Let's see this in action on some examples.

Example 1

Solve the system of linear equations:

Step 1: Make one variable the subject of one of the equations:
It's easiest to do this with equation 1 to give:

after adding \(y\) to both sides of the equation.

Step 2: Replace \(x\) by \(5 + y\) in the other equation (equation 2):

Step 3: Solve this equation for \(y\):

So \(y = -2\).

Step 4: Plug this \(y\)-value into \(x = 5 + y\) to complete the solution:

So the solution is \(x = 3\) and \(y = -2\). We can see this as the point \((3,-2)\) of intersection of the two lines on the graph below:

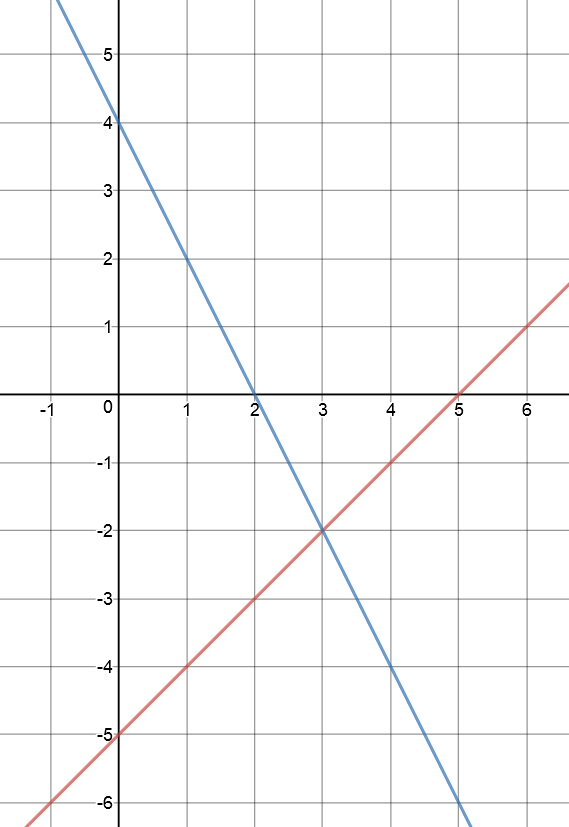
Note: Because there is a solution, the equations are consistent. However, you should always check that your solution works for both equations. I'll leave that up to you.

Next, we'll try a system with 3 equations.

Example 2

Solve the system of linear equations:

It's a good idea to line up the variables in columns so that you can keep track of what you're doing:

Step 1: Make one variable the subject of one of the equations (it doesn't matter which equation or which variable):
It's easiest to do this with equation 1 to give:

after adding \(z\) to both sides of the equation.

Step 2: Replace \(x\) by \(4 + z\) in the other equations (equations 2 and 3):

Step 3: Solve these equations for \(y\). Equation 2:

Equation 3 becomes:

Next, choose one of these expressions to plug into the other equation. Again, it doesn't matter which, but I chose \(y = 71 - 7z\) because it didn't include a fraction:

Now, plug \(z = 10\) into your expressions for \(x\) and \(y\) to give:

So the equations are consistent and the solution is \(x = 14\), \(y = 1\) and \(z = 10\), which may be written as the point \((14,1,10)\). You should plug these values into the three equations to make sure they work for all three equations.

Conclusion

Finding the solution to the system of three equations involved a bit of extra mucking around. Sometimes, for systems of three or more equations, it's more efficient to use the elimination technique rather than the substitution technique. You can use substitution for systems of 4, 5 or as many equations as you like, it just takes a long time. In fact, I rarely ever use substitution.

The elimination technique takes a bit of getting used to, but it can be more efficient. You can find out about it in the article on solving systems of equations by elimination.