Finding the Graph for an Equation

The graph for an equation is the set of points at which the equation is satisfied (that is, the \(x\) and \(y\)-values that work!).

Let's look at a few examples.

Example 1

To find the graph of the equation \(y= 2x + 1\), we start by plotting some points at which the equation is satisfied:

\(x\)	\(y = 2x + 1\)
\(-2\)	\(-3\)
\(-1\)	\(-1\)
\(0\)	\(1\)
\(1\)	\(3\)
\(2\)	\(5\)

Most of the time, this will give us a good idea of what the graph of the equation should look like. However, it's good if you can figure out some of the other properties of the equation as well. For example, we know that this equation will have a straight line as its graph because it is linear (the only power of \(x\) is \(x^1\)).

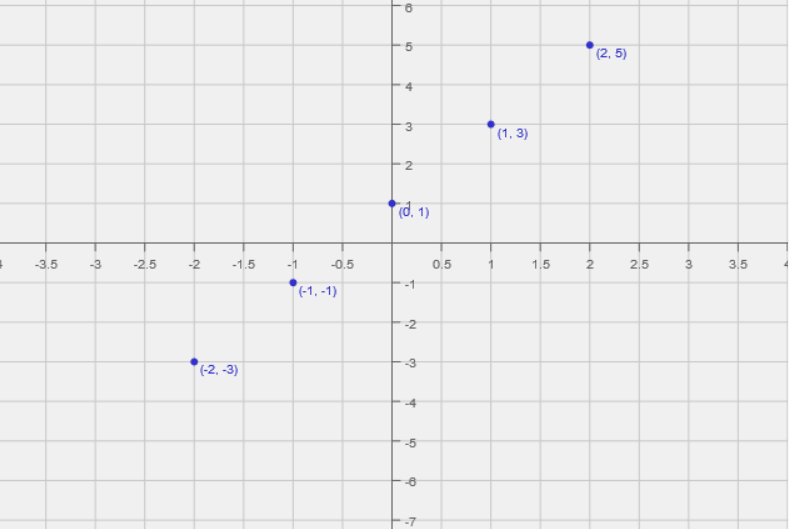
In this example, joining all these points will give the graph of the function, which is the set of all points satisfying the equation. Of course, we can only show a finite section of the graph. This graph will go on forever in both directions. Here's part of the graph of the equation \(y = 2x + 1\):

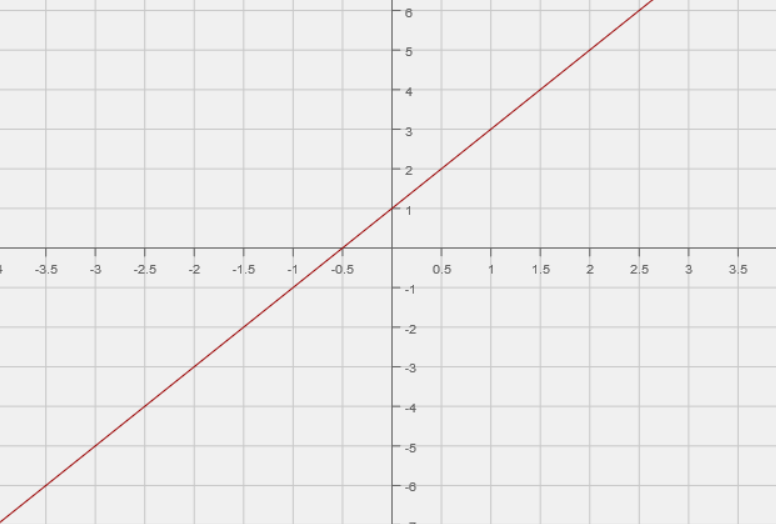
Example 2

To find the graph of the equation \(y= x^2 - 3\), we also start by plotting some points at which the equation is satisfied:

\(x\)	\(y = x^2 - 3\)
\(-2\)	\(1\)
\(-1\)	\(-2\)
\(0\)	\(-3\)
\(1\)	\(-2\)
\(2\)	\(1\)

Most of the time, this will give us a good idea of what the graph of the equation should look like. However, it's good if you can figure out some of the other properties of the equation as well. For example, we know that this equation will have a parabola as its graph because it is quadratic (the highest power of \(x\) is \(x^2\), and all powers of \(x\) are positive integers).

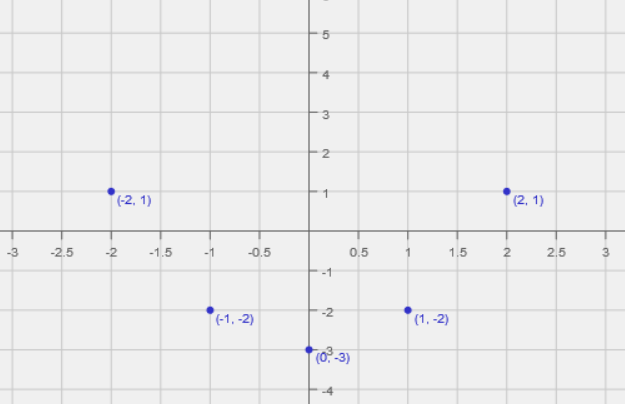
In this example, these points and our knowledge of the graph of equations like this give us a good idea of the graph of the function, which is the set of all points satisfying the equation. Of course, we can only show a finite section of the graph. It is best to plot as many points as possible. This graph will extend forever upwards. Here's part of the graph of the equation \(y = x^2 - 3\):

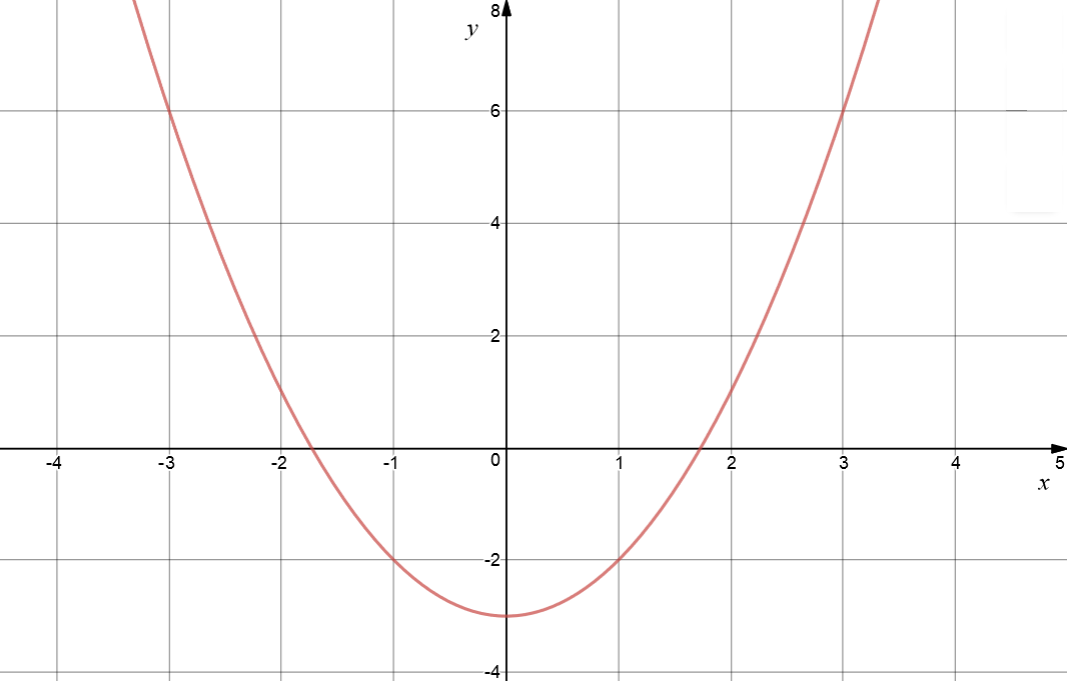
Now let's look at an example in which plotting just a few points can be misleading.

Example 3

To find the graph of the equation \(y= x^3 - 2x + 2\), we also start by plotting some points at which the equation is satisfied. If we start with just these points

\(x\)	\(y = x^3 - 2x + 2\)
\(-2\)	\(-2\)
\(0\)	\(2\)
\(2\)	\(6\)

we might think that the graph is a straight line like the dotted line on the right. However, we'd be wrong. If you don't really know what the graph should look like, it's a good idea to plot quite a few points. It's even better if you can figure out some properties of the equation that might help you. For example, this is a cubic equation (the highest power of \(x\) is \(x^3\)), so we know that its graph will cut the \(x\)-axis at most three times. We also know that its graph is going to be curvy, so a straight line isn't correct.

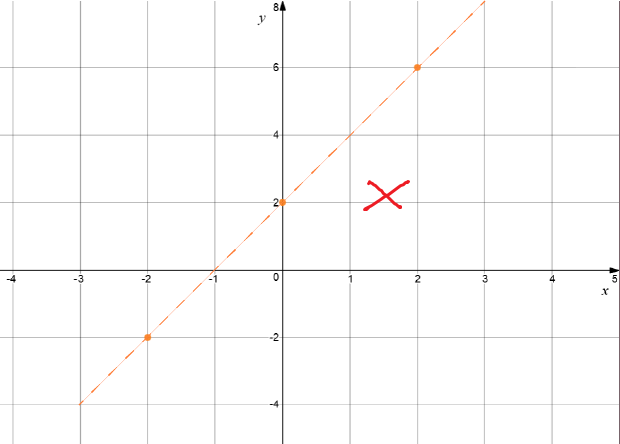
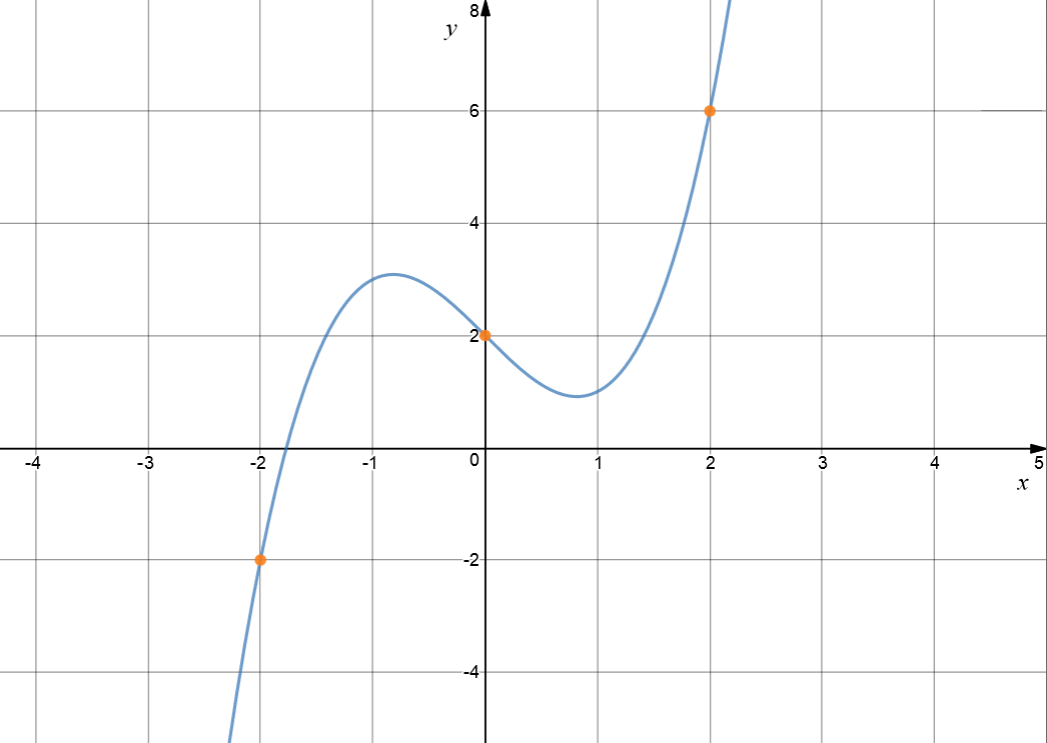
If we'd plotted a few more points satisfying the equation before we tried to draw the graph, we'd have realised that the graph actually looks more like this:

More Suggestions for Graphing Equations

If you get really stuck, you can use one of the many free on-line graphing calculators that are available. I like Desmos and GeoGebra, but there are quite a few of them. It's good to play around with them to get an idea of what the graphs of various types of equations look like.

It's also a good idea to learn to recognise the equations of some common types of graphs like straight lines, parabolas and circles.

A really good graph of an equation should include the following features:

• \(x\) and \(y\)-intercepts.
• Maximum values (peaks)
• Minimum values (valleys)
• Any areas where the graph plateaus (is flat)
• Asymptotes (lines that the graph gets as close as you like to, but never crosses)
• Any gaps or jumps
• A few plotted points
• Where is the graph increasing (going uphill) or decreasing (going downhill)?
• What happens to the graph for very large and very small values of \(x\)?
• Any other special features of the equation

In Years 11 and 12, you'll learn about Calculus. Calculus provides you with a wonderful tool kit for finding the important features of equations, and so will help you to draw their graphs.