Year 10+ Coordinate Geometry
Chapters
Equations and Formulas
Equations and Formulas
Equations
Equations are mathematical expressions that say that two things are equal. Equations always include equals signs \(``="\). For example,
So, an equation is a type of mathematical sentence which includes `equals' as its verb.
The equation above has the solution, \(x = 5\). There's an article about solving equations that will take you through the steps of finding this solution.
Formulas
Formulas are equations satisfying a special property. They not only have to include 'equals', they have to include two or more variables. Variables are symbols
like \(x\), \(y\), \(V\) and \(h\) that can take on many different values. They always take the place of numbers.
For example
- \(V = lwh\) is a formula
- \(S = ut + \dfrac{1}{2}at^2\) is a formula
- \(y = 3x + 7\) is a formula
- \(x = 3x - 4\) is an equation, but not a formula as it only includes the one variable, \(x\).
Example 1
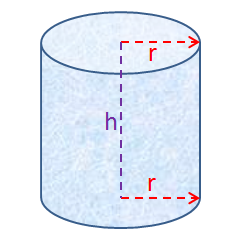
The volume of a cylinder is given by the formula:
For example, when \(r = 2\) and \(h= 3\), \(V= \pi (2)^2 (3) = 12 \pi \text{ units}^3\). When \(r = 3\) and \(h = 2\), \(V = \pi (3)^2(2)= 18 \pi \text{ units}^3\).
Example 2
Mathematicians often develop formulas to model real world situations like this one.

The eminent maths professor, Gus the snail has been monitoring the invasion of his garden by hordes of feral caterpillars. He has investigated the relationship between the number of cabbages in his garden and come up with the following formula to model it:

The Subject of a Formula
The subject of a formula is a variable that sits on its own on one side of the formula (usually the left). It is followed by an equals sign, and the other side of the formula (usually the right) includes an expression in the remaining variables that tells you what the subject is equal to.
For example, the subject of Gus the snail's formula:
The subject of the formula:
Changing the Subject of a Formula
One important use of algebra is that it gives us the ability to rearrange a formula to make a different variable its subject. Let's finish off by looking at some examples.
Example 1
Gus the snail is now interested in the number of moths in his garden. He needs to make moths the subject of his formula:
Example 2
Suppose we want to find the required height to produce a cylinder of base radius \(2 \text{ cm}\) and volume \(20 \pi \text{ cm}^3\). We need to make \(h\) the subject of the volume formula:
- Start with \(V = \pi r^2 h\)
- Divide both sides by \(\pi\) to give \(\dfrac{V}{\pi} = r^2 h\).
- Divide both sides by \(r^2\) to give \(\dfrac{V}{\pi r^2} = h\).
- Change the sides over so that \(h\) is on the left: \(h = \dfrac{V}{\pi r^2}\).
Now we can apply our new formula for the height of a cylinder to calculate:
Description
A coordinate geometry is a branch of geometry where the position of the points on the plane is defined with the help of an ordered pair of numbers also known as coordinates. In this tutorial series, you will learn about vast range of topics such as Cartesian Coordinates, Midpoint of a Line Segment etc
Audience
year 10 or higher, several chapters suitable for Year 8+ students.
Learning Objectives
Explore topics related to Coordinates Geometry
Author: Subject Coach
Added on: 27th Sep 2018
You must be logged in as Student to ask a Question.
None just yet!