Systems of Linear Equations

Linear Equations

Linear Equations are equations in which every term is either a constant or the product of a constant with a single variable that is raised to the power \(1\). In 2-dimensional space, they are the equations with graphs that are straight lines.

For example, these are all linear equations:

• \(y = x\)
• \(y = 3\)
• \(y = 3x + 4\)
• \(15 x = 6y + 7\)
• \(\dfrac{1}{3}\;y = 12 x - 6\)

and this is the graph of a linear equation

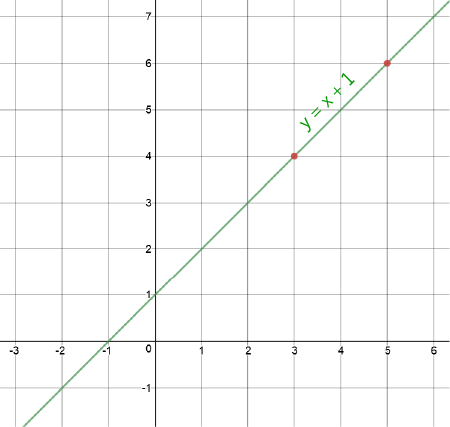
We can write linear equations in 2, 3, 4 or as many dimensions (or numbers of variables) as well like. They just have obey the rule that every term is either a constant or the product of a constant with a single variable that is raised to the power \(1\).

For example,

• \(x + y - 3z = 7\)
• \(2x + 3y - 4z + w = 5\)
• \(-3x + 5y + s + t + u = 15\)

are all linear equations, but

• \(x^2 + y - 3z = 7\)
• \(2x + 3\sqrt{y} - 4z + w = 5\)
• \(-3x + 5y + zws + t + u = 15\)

are not.

The number of variables in the equations of the system determines the dimension of the space that they lie in.

In 3-dimensional space, linear equations can represent lines or planes:

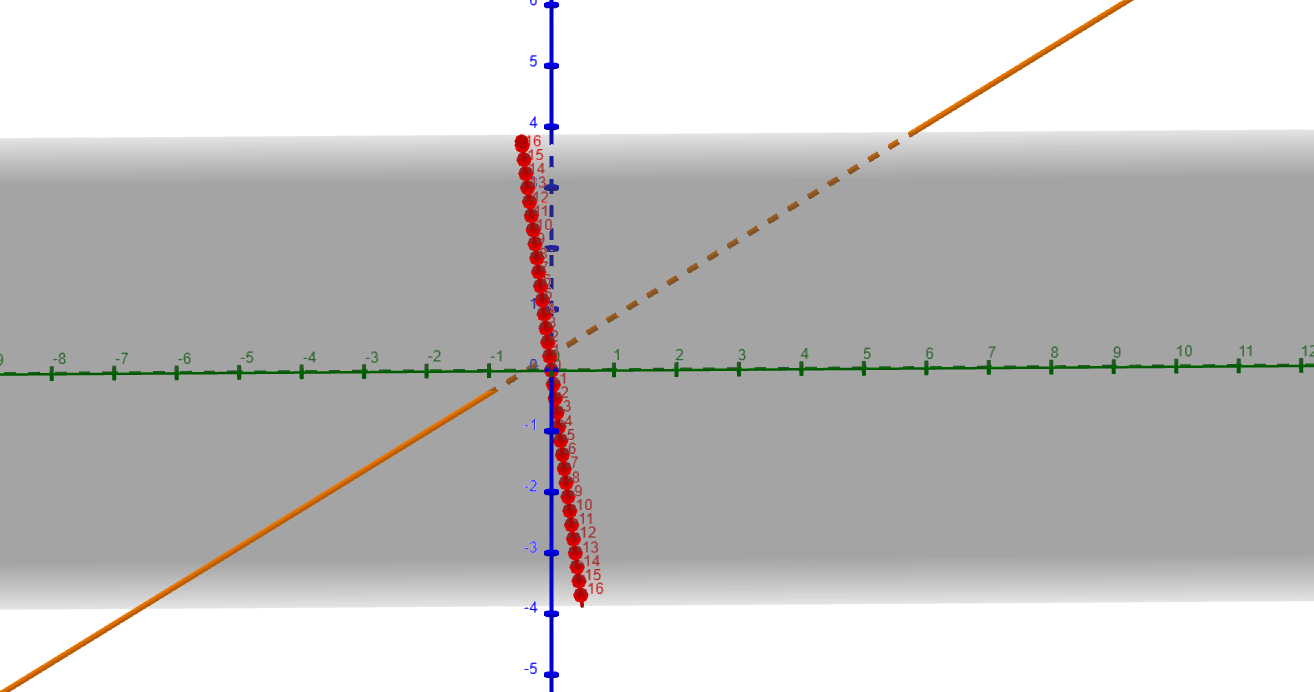
Systems of Linear Equations

Sometimes we might be asked to think about two or more linear equations at the same time. This is called a system of linear equations.

Example

In order for a collection of linear equations to form a system, all of the equations must share the same (or at least some of the same) variables.

For example, here is a system of linear equations in 4 variables:

The above system of linear equations includes 4 equations in the 4 variables \(x,y,z\) and \(w\). They all share the same variables, but some of the variables are missing from some of the equations. This is fine: they are really there, they just have coefficients of zero.

Systems of linear equations can have any combination of numbers of equations and numbers of variables. There are no particular rules except:

• There must be more than 1 equation.
• All the equations must be linear.
• All the equations must share the same variables.

Let's talk about the sorts of solutions that a system of linear equations can have. A solution to a system of linear equations must satisfy every equation in the system.

Solutions of Systems of Linear Equations

As we said, the solutions of systems of linear equations correspond to points of intersection of the lines whose equations are the linear equations in the system.

Let's think about what can happen if we have two straight lines. For now, we'll just work in 2-dimensional space. How many points of intersection can they have?

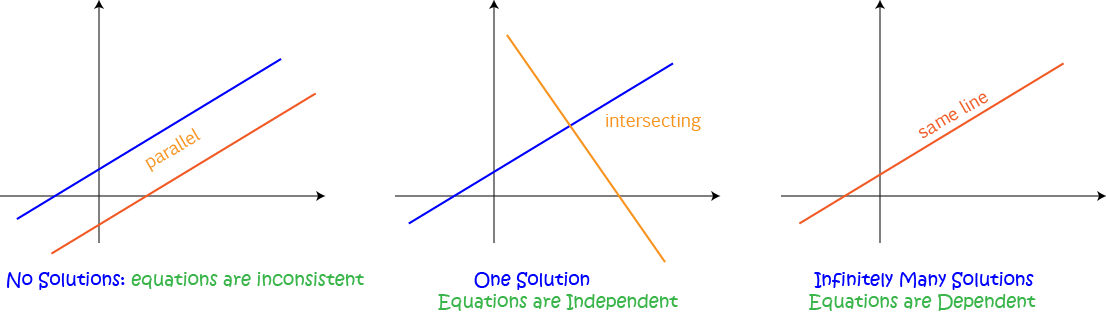
• If the two lines are parallel, then they have no points of intersection as they never cross. The system of linear equations made up of the equations of the two lines has no solutions.
• The two lines might intersect at a point. The system of linear equations made up of the equations of the two lines has one solution.
• If the two lines intersect at more than one point, then they must be the same straight line. We say that the system of linear equations made up of the equations of the two lines has infinitely many solutions.

If a system of linear equations has no solutions, then we say that the equations are inconsistent: they can't all be satisfied at the same time.

In all other cases, we have a consistent system of linear equations.

There are two more terms that are used when talking about systems of linear equations. These are independent (or linearly independent) and dependent (or linearly dependent).

A system of linear equations is independent if each equation in the system provides new information: you can't build any of the equations out of the other equations in the system. A system of equations is dependent if it is not independent. I realise that's a double negative, but it's the best way to describe it. In other words, a system of equations is dependent if you can build one or more equations in the system out of the other equations in the system. Let's look at some examples.

Example 1

The equations

are dependent because we can build the second equation by multiplying the first equation by 3. So, the second equation gives no new information.

Example 2

The equations

are dependent because we can build the third equation by adding the first two equations together. So, the third equation gives no new information.

Gus and Alyce

Now let's check out the situation with Gus and Alyce. There are two problems to consider:

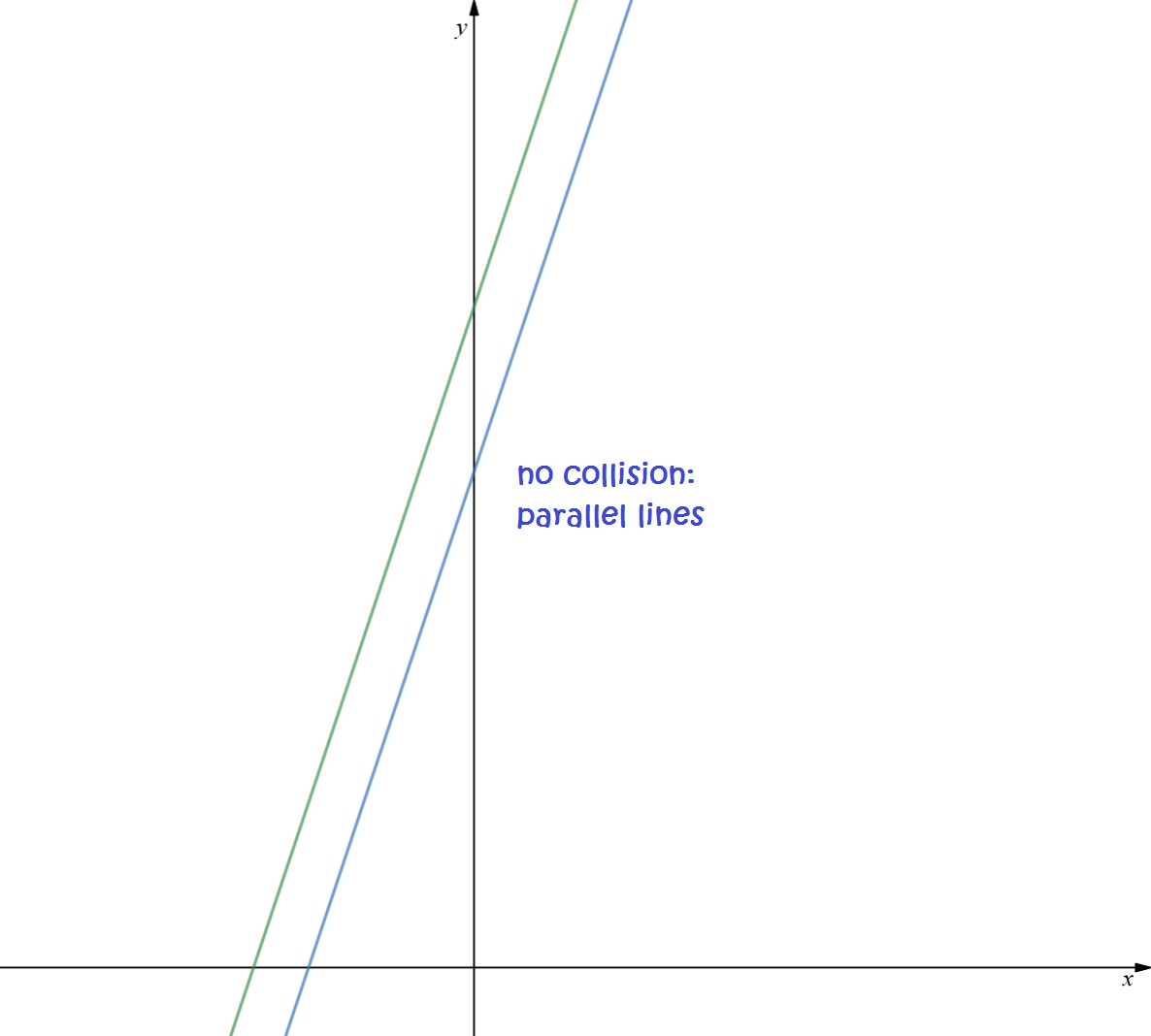
1. If Gus glides along the line \(y = 3x + 3\) and Alyce glides along the line \(y = 3x + 4\), will they crash into each other if they continue along their current routes?
2. The next day, Gus glides along the line \(y = 3x - 3\) and Alyce glides along the line \(y = 2x + 1\). Will they crash into each other?

If we plot the graphs for question 1, we see that the two lines are parallel. So, the equations are inconsistent (they can't both be satisfied at the same time) and the snails will never collide:

.

The situation is different in question 2. The two lines have a single point of intersection (the system is independent - both equations given new information) and the snails collide at that point:

.

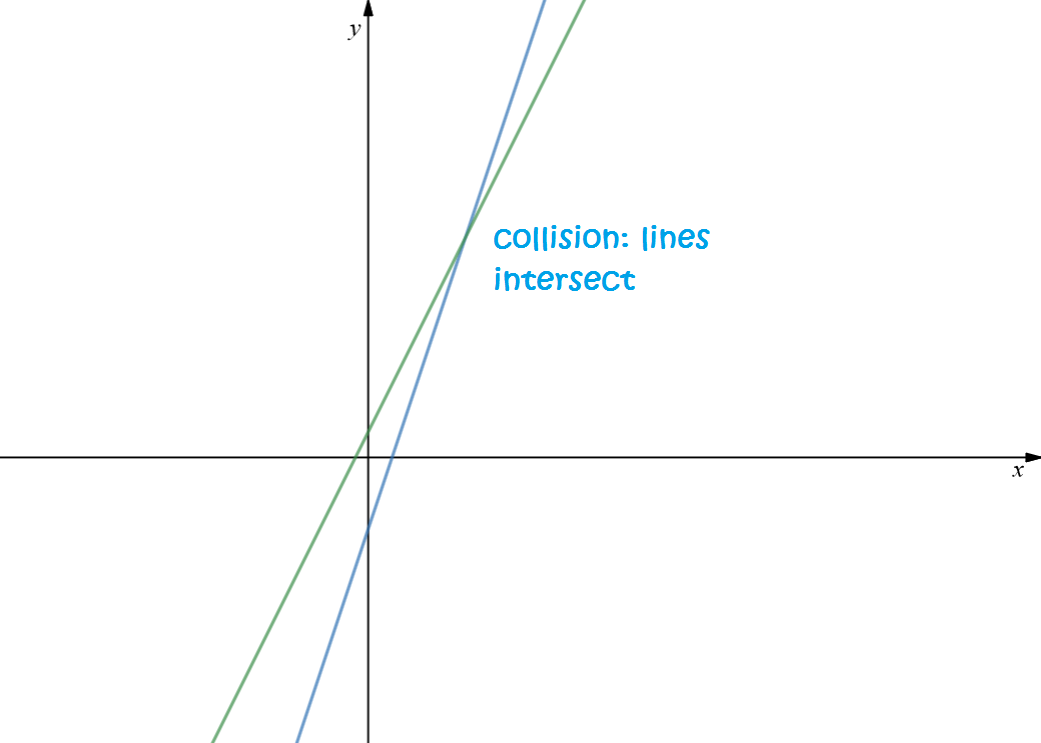
In fact, both of these equations are satisfied at the point where \(x = 4\) and \(y = 9\). We call the point \((4,9)\) the solution of the system of equations. This is the point at which Gus and Alyce crash into each other. I hope they're not going too fast!

When we have a system of two linear equations in two unknowns, we can often read the solution from their graphs (if we draw them carefully). Otherwise, we need to use algebra. Two of the techniques that can be used for solving systems of linear equations are called substitution and elimination. We'll talk about these in the articles about solving systems of linear equations by elimination and solving systems of linear equations by substitution.