Point-Gradient Equation of a Straight Line

If you know the gradient (slope) of a straight line, and a point that the line passes through, then you can write down the equation of the line straight away. It is

The Variables in the Above Equation

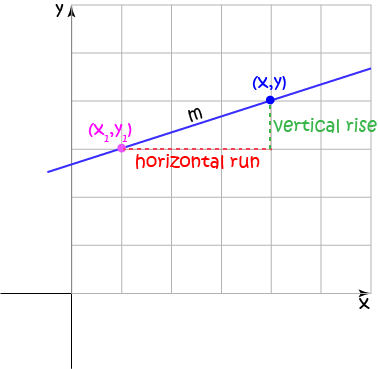
In the equation

\(y - y_1 = m(x - x_1)\)

• \(m\) is the gradient (slope) of the line
• \((x_1,y_1)\) is the point on the line that you know about.
• \((x,y)\) is another point on the line. It is allowed to move freely along the line. The equation tells us all the possible values of \((x,y)\).

Where does the Point-Gradient Equation Come From?

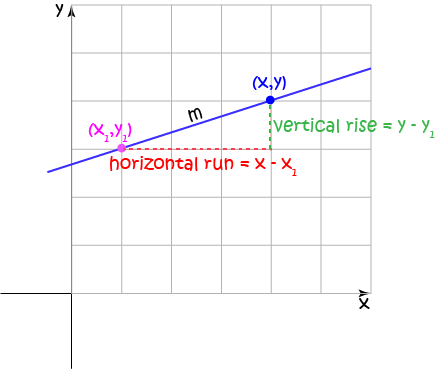
It is based on the definition of the gradient (slope). Remember that

\(m = \dfrac{\text{vertical rise}}{\text{horizontal run}}\)

In our picture, this is the same as saying

\(m = \dfrac{{y - y_1}}{{x - x_1}}\)

Rearranging (multiplying both sides by \((x - x_1)\)) gives the equation:

\(y - y_1 = m(x - x_1)\)

So, the Point-Gradient equation is just the formula for the gradient of the line, rearranged.

Let's use it in anger on a few examples.

Example 1

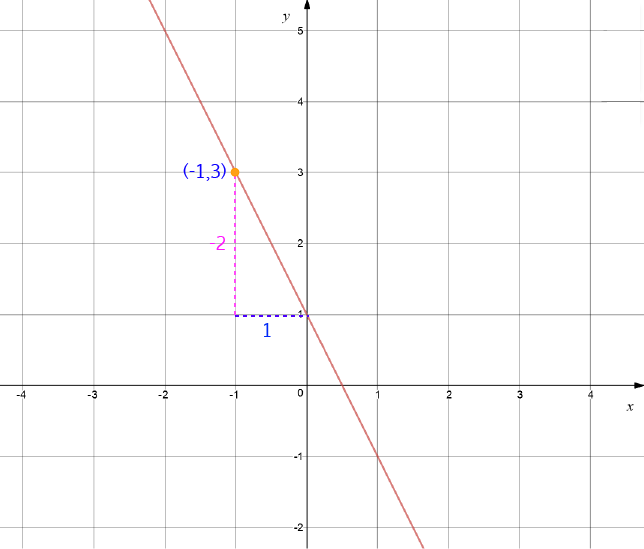
This line is sloping downhill, so its gradient is negative.

\(m = \dfrac{\text{vertical rise}}{\text{horizontal run}} = \dfrac{-2}{1} = -2\)

and the point that it passes through is \((-1,3)\). So, the equation is

\(y - 3 = -2( x - (-1)),\)

which we can rearrange to give:

\(\begin{align*} y -3 &= -2( x + 1)\\ y - 3 &= -2x -2 \\ y &= -2x + 1 \end{align*} \)

Example 2

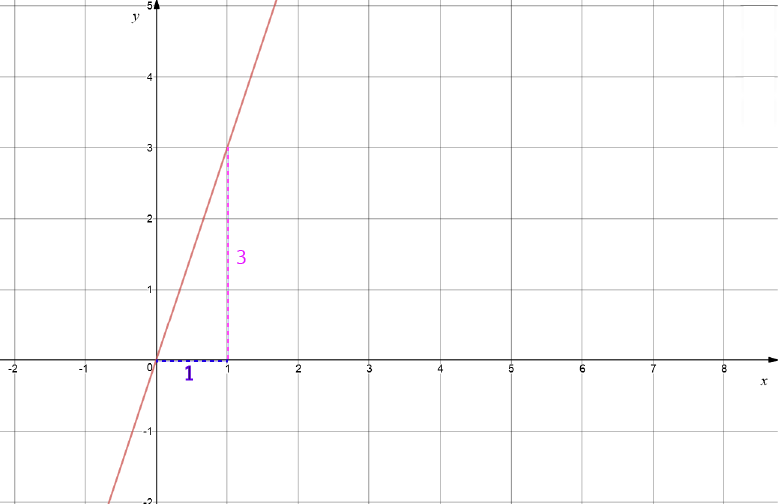
This line is sloping uphill, so its gradient is positive.

\(m = \dfrac{\text{vertical rise}}{\text{horizontal run}} = \dfrac{3}{1} = 3\)

and a point that it passes through is \((0,0)\). So, the equation is

\(y - 0 = 3( x - 0),\)

which we can simplify to give:

\(\begin{align*} y - 0 &= 3( x - 0)\\ y &= 3x \end{align*} \)

Example 3 (Horizontal Line)

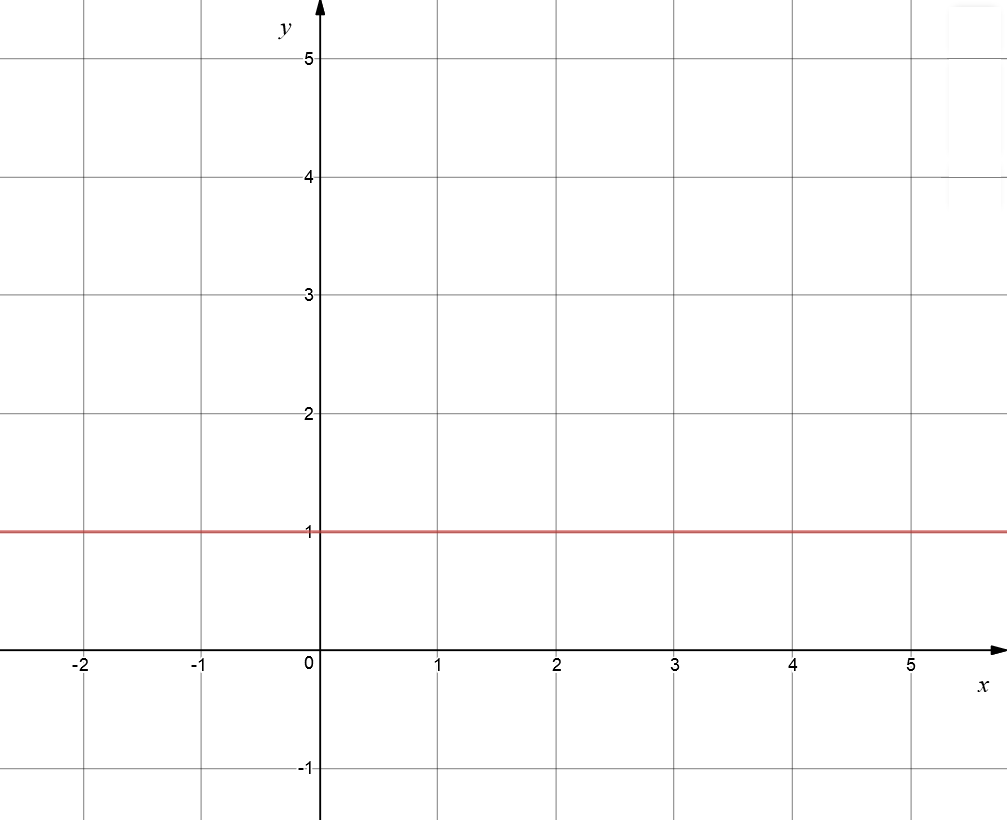
This line is horizontal, so its gradient is zero.

\(m = 0\)

and a point that it passes through is \((7,1)\). So, the equation is

\(y - 1 = 0( x - 7),\)

which we can rearrange to give:

\(\begin{align*} y -1 &= 0\\ y &= 1 \end{align*} \)

Example 4 (A Vertical Line)

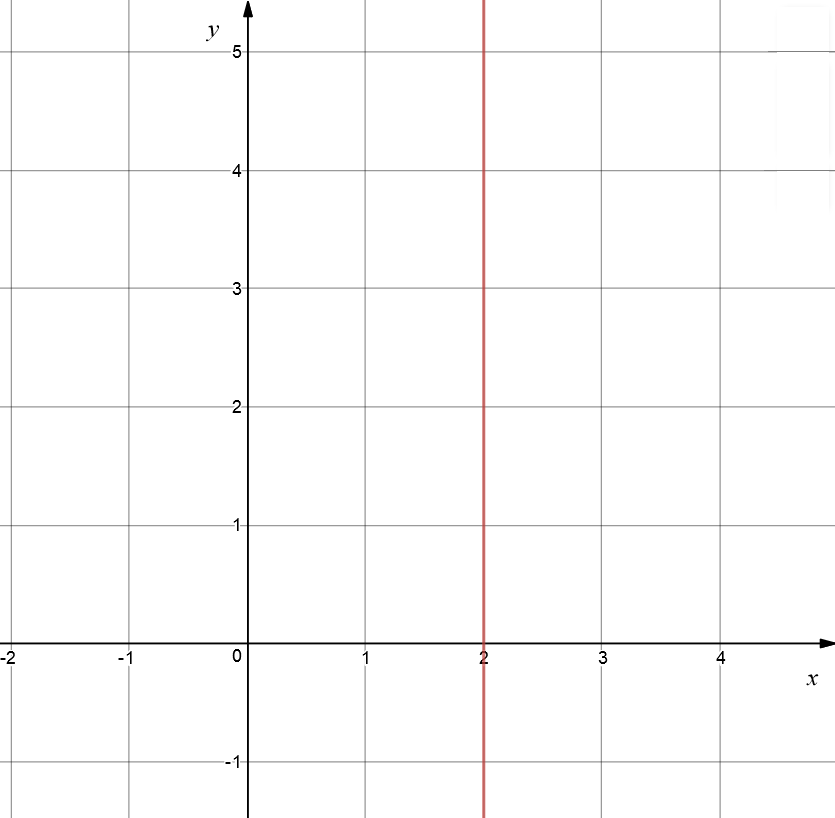
Unfortunately, the gradient of a vertical line is undefined. So, we have to get a bit cleverer here.

In fact, we have to invent a whole new type of equation for vertical lines. The equation of a vertical line through \(x = a\) is just \(x = a\), so the equation of our line is

\( \begin{align*} x = 2. \end{align*} \)

How Do We Get \(y = mx+b\) Back?

I'm a bit stubborn. I really love the \(y = mx + b\) form of the equation of a straight line. So much so, that every time someone gives me a new version of the equation of a straight line, I have to work on it to see that I can get \(y = mx + b\) back again!

This one is not so hard. If our gradient is \(m\) and our \(y\)-intercept is \(b\), then we know that our line passes through the point \((0,b)\). So, we'll set \((x,y) = (0,b)\) and plug it into the Point-Gradient form of the equation. Here goes!

So, I'm happy! This gives me back \(y = m x + b\).

Conclusion

Now it's time to go and play with some straight line graphs. See if you can work out their equations.

You can also work the other way around and see what straight line graphs different equations will give you. The article on exploring the equation of a straight line will get you started here. After that, I'd suggest trying out an on-line graphing calculator like Desmos or Geogebra and testing the effects of different values of \(m\) and passing through different points. Have fun!