Year 10+ Coordinate Geometry
Chapters
Linear Equations
Linear Equations
Linear Equations are equations in which every term is either a constant or the product of a constant with a single variable that is raised to the power \(1\). They
are the equations with graphs that are straight lines.
For example, these are all linear equations:
- \(y = x\)
- \(y = 3\)
- \(y = 3x + 4\)
- \(15 x = 6y + 7\)
- \(\dfrac{1}{3}\;y = 12 x - 6\)
These are not linear equations:
- \(y = x^2 + 6\)
- \(y^2 = x + 7\)
- \(y = \sqrt{x + 3}\)
- \(y = 2^x + 3\)
- \(y = \sin(x + 4)\)
If an equation includes a power of \(x\) other than \(x^1 = x\) or \(x^0 = 1\), a square root, a sine, a cosine, an exponential etc, it is not linear.
Example
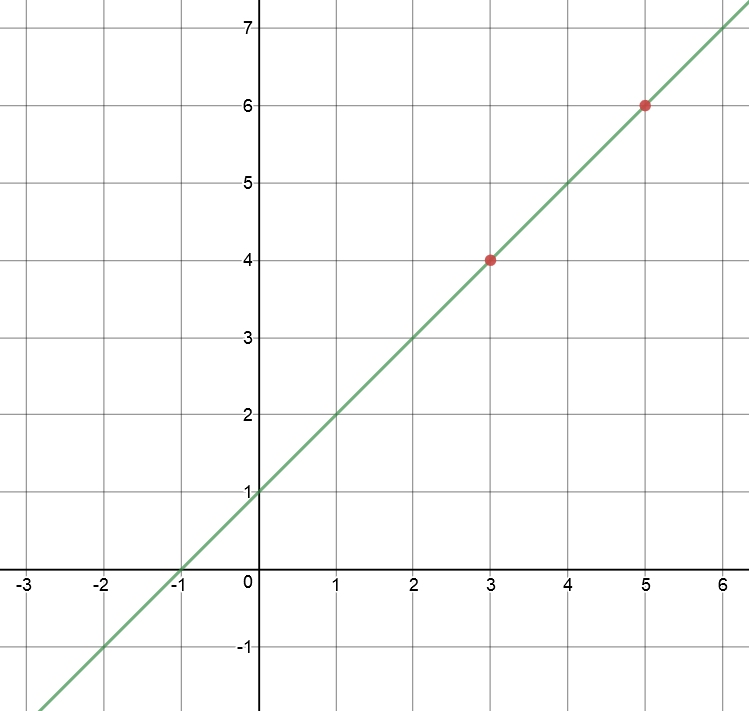
\(y = x + 1\) is a linear equation.
- Its graph is a straight line.
- \(y\) increases at the same rate as \(x\).
- When \(x\) is \(0\), \(y = 1\), so we need to add on a \(1\) to the equation \(y = x\).
Here is a table of some of the values of \(y\) for different \(x\)-values:
| \(x\) | \(y = x + 1\) |
|---|---|
| \(-2\) | \(-2 + 1 = -1\) |
| \(-1\) | \(-1 + 1 = 0\) |
| \(0\) | \(0 + 1 = 1\) |
| \(1\) | \(1 + 1 = 2\) |
| \(2\) | \(2 + 1 = 3\) |
Different Forms of Linear Equations
Linear equations have a number of different possible forms. All include constants (like 0 or -236), and the variables are only ever raised to the power \(1\).
Here are some different ways of writing the linear equation \(y = x + 1\):
- \(y = x + 1\) (gradient-intercept form)
- \(y - 1 = 1(x - 0)\) (point-gradient form)
- \(\dfrac{y - 1}{5 - 3} = \dfrac{x - 0}{4 - 2}\) (2 point form)
- \(x - y + 1 = 0\) (general form)
Gradient-Intercept Form
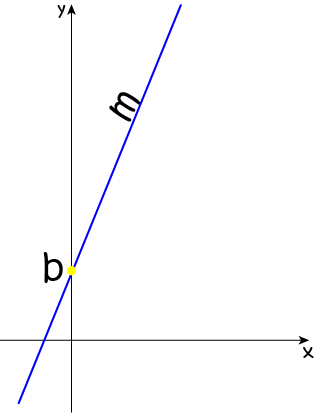
This equation has the form
This is probably the most common form of the equation of a straight line and, indeed, you can do anything you need to do with linear equations using this form. Your textbook will give you a few other forms to work with.
For example,
- \(y = x + 1\) is in this form: \(m = 1\) and \(b = 1\).
- \(y = 3x - 4\) is also in this form: \(m = 3\) and \(b = -1\).
If you read the article on exploring the graph of a straight line equation, you will see the effects of changing the values of \(m\) and \(b\) on the graph. Better yet, have a play on an on-line graphing calculator and see how you can change the graph by changing the values of \(m\) and \(b\).
Point-Gradient Form
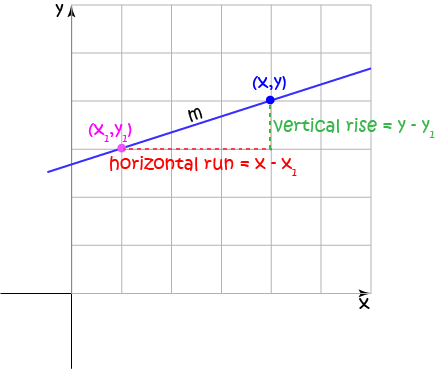
Sometimes we're told the gradient of a line, and a point that it passes through. We can use this information to find a linear equation of the form
For example, the equation of a line with gradient \(3\) that passes through the point \((1,4)\) is
The equation \(y - 2 = -7 (x + 4)\) is in point-gradient form with
- gradient (or slope) -7
- \(x_1 = -4\) and
- \(y_1 = 2\).
Two Point Form
Two points are enough to nail down a linear equation. If the points are \((x_1,y_1)\) and \((x_2,y_2)\), then the equation is
For example, the linear equation satisfied by both the points \((3,4)\) and \((5,6)\) is
General Form
Sometimes we are asked to put linear equations into general form. This is particularly relevant when we need to do matrix operations to manipulate systems of linear equations. We'll talk more about that in the articles on matrices.
Here's the general form of the equation of a straight line. The \(A\), \(B\) and \(C\) are constants, and \(A\) and \(B\) can't both equal zero. Note that the term in \(x\) comes first:
For example, the equation \(2x + 3y - 5 = 0\) is in general form with
- \(A = 2\)
- \(B = 3\)
- \(C = -5\)
Function Notation
It is common to see linear equations written in function notation. Some examples include:
- \(f(x) = -2x + 4\)
- \(g(q) = 3q - 2\)
- \(h(a) = 17a - 254\)
The Identity Function
Sometimes we call the linear equation \(f(x) = x\) the identify function because it doesn't change \(x\) at all. \(x\) maintains its "identity".
The graph of the identify function looks like this:
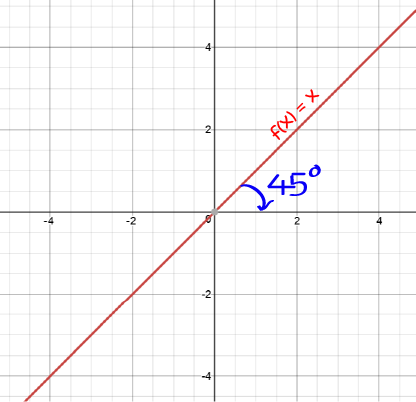
Constant Functions
Constant functions are also linear equations. Of course, only one of the variables can be kept constant, or you'd just get a point.
The graphs of \(f(x) = \text{constant}\) look like this:
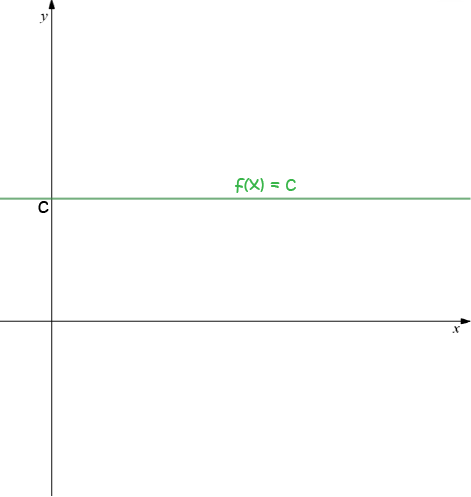
The graphs of \(x = \text{constant}\) are vertical lines.
Some examples of constant equations are
- \(f(x) = 17\): the points satisfying this equation are \((1,17), (243,17), (-23,17), (\text{anything you like}, 17)\).
- \(x = 2\): the points satisfying this equation are \((2,-243),(2,0), (2,27), (2,\text{anything you like})\).
Conclusion
That's all I have to say about linear equations for now. You might like to have a read about the ways you can use linear equations to tell whether lines are parallel or perpendicular, or to find out how you solve systems of linear equations in some of the other articles. Have fun!
Description
A coordinate geometry is a branch of geometry where the position of the points on the plane is defined with the help of an ordered pair of numbers also known as coordinates. In this tutorial series, you will learn about vast range of topics such as Cartesian Coordinates, Midpoint of a Line Segment etc
Audience
year 10 or higher, several chapters suitable for Year 8+ students.
Learning Objectives
Explore topics related to Coordinates Geometry
Author: Subject Coach
Added on: 27th Sep 2018
You must be logged in as Student to ask a Question.
None just yet!