Year 10+ Coordinate Geometry
Chapters
Equations of Circles
Equations of Circles
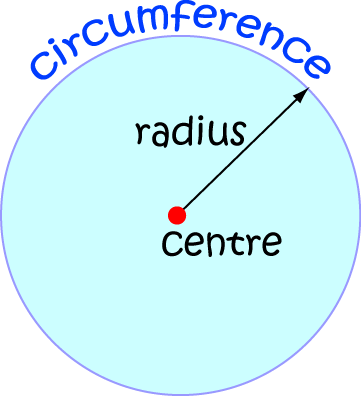
Formally, mathematicians define a circle to be the locus of a point which moves so that it is a fixed distance away (called the radius)
from a fixed point called the centre.
We need to come up an equation that tells us that the distance of point \((x,y)\) from the centre of the circle is always equal to the same constant.
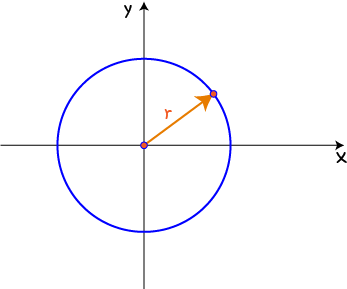
The Equation of a Circle, Centred at the Origin
If we draw a circle of radius \(r\), centred at the origin, in the \(xy\)-plane, we end up with the graph below:
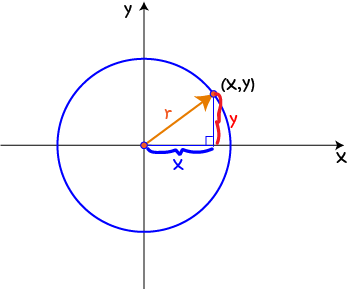
We need to work out how to use algebra to say, exactly, where every point \((x,y)\) lies as it moves around the circle. We'll start by looking at the coordinates of the point. We draw a right-angled triangle with sides of length \(x\) and \(y\), corresponding to the \(x\) and \(y\)-coordinates of \((x,y)\), and hypotenuse of length equal to the radius of the circle:
Example
Let's find some points on the circle \(x^2 + y^2 = 9\). This is the equation of a circle, centre the origin, radius \(3\). There are infinitely many points on the circle, but we'll only locate a few.
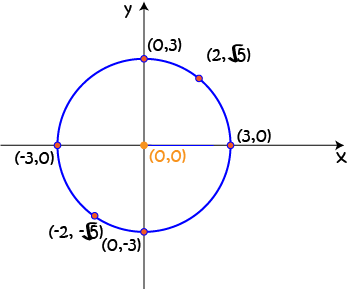
| \(x\) | \(y\) | \(x^2 + y^2\) |
|---|---|---|
| \(3\) | \(0\) | \(3^2 + 0^2 = 9\) |
| \(2\) | \(\sqrt{5}\) | \(2^2 + (\sqrt{5})^2 = 9\) |
| \(0\) | \(3\) | \(0^2 + 3^2 = 9\) |
| \(-3\) | \(0\) | \((-3)^2 + 0^2 = 9\) |
| \(-2\) | \(-\sqrt{5}\) | \((-2)^2 + (-\sqrt{5})^2 = 9\) |
| \(0\) | \(-3\) | \(0^2 + (-3)^2 = 9\) |
All of these points satisfy the equation: \(x^2 + y^2 = \text{radius}^2\).
Example
Find all points on the circle \(x^2 + y^2 = 25\) with \(x\)-coordinate \(3\).
Solution:
We plug \(x = 3\) into the equation and solve for \(y\):
So, the points are \((3,4)\) and \((3,-4)\).
What if the Centre is Somewhere Else?
Let's move the centre to the point \((h,k)\).
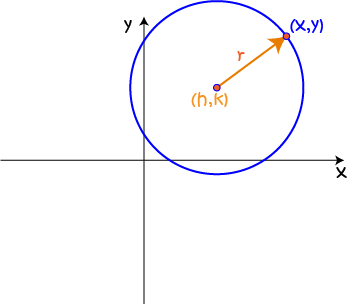
We need to work out how to use algebra to say, exactly, where every point \((x,y)\) lies as it moves around the circle. All points must be distance \(r\) away from the centre \((h,k)\). We'll start by looking at differences between the coordinates of \((x,y)\) and the coordinates of the centre. We draw a right-angled triangle with sides of length \(x -h \) (for the distance between the two \(x\)-coordinates) and \(y - k\) (for the distance between the two \(y\)-coordinates). The hypotenuse of the right-angled triangle will have length equal to the radius of the circle:
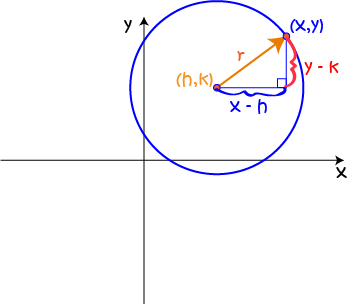
standard form of the equation of a circle.
When the equation of a circle is in standard form, we can read off the co-ordinates of its centre, and quickly find its radius.
Example
Find the equation of a circle with centre \((23, 35)\) and radius \(13\).
Solution:
We use the standard form of the equation of the circle:
General Form of the Equation of a Circle
Sometimes we are given equations in general form, and asked to determine what they represent. The general form of the equation of a circle looks like this:
Note: the general form of the equation of a circle should start with \(x^2 + y^2\) as its first two terms. That's how you recognise it as a circle. Sometimes you might be given an equation which starts with \(Dx^2 + Dy^2\), where \(D\) is some non-zero constant. If you divide both sides by \(D\), you'll end up with an equation that starts with \(x^2 + y^2\) and you'll be back in circle territory. If you're given equation that starts with \(Dx^2 + Ey^2\), where \(D\neq E\), then it is not the equation of a circle.
Example: Converting an Equation from Standard Form to General Form
Let's start with the equation \((x - 3)^2 + (y - 4)^2 = 5^2\) and convert it into general form.
Step 1: Expand it out:
Step 2: Pull all the constant terms together:
Step 3: Put the \(x^2 + y^2\) at the front, then the terms in \(x\) and \(y\) in the right order:
Example: Converting from General Form to Standard Form
To do this, we need to complete the square twice: once for \(x\) and once for \(y\).
Let's convert the equation \(x^2 + y^2 - 4x + 8y - 11 = 0\) to standard form.
First, pull all the terms in \(x\) together and all the terms in \(y\) together:Next, complete the square for \(x\): take half the coefficient of \(x\), square it and add it to both sides of the equation:
Next, complete the square for \(y\): take half the coefficient of \(y\), square it and add it to both sides of the equation:
Simplify and write the terms in \(x\) and \(y\) as perfect squares:
Unit Circle
A very important circle has centre \((0,0)\) and radius \(1\). We call it the unit circle and it looks like this:
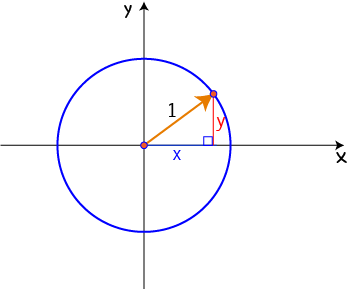
If you know some trigonometry, you can read all about this circle in the article on the unit circle.
Hand-Plotting a Circle
It's next to impossible to draw a circle by hand, but this should help a bit. If you have to draw a circle by hand for a test, don't panic. Just follow these steps and do the best you can.
- Plot the centre.
- Plot 4 points, one directly to the right, one directly to the left, one directly above, and one directly below the centre.
- Join them up with round curvy circle-like lines. Just do your best!
Example
Plot \((x - 3)^2 + (y - 2)^2 = 16\).
This is the equation of a circle, with centre \((3,2)\) and radius \(\sqrt{16} = 4\).
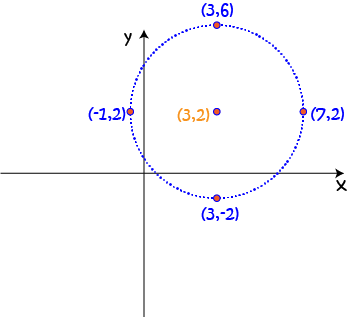
We plot
- The centre, \((3,2)\).
- A point directly above it: \((3,2 + 4) = (3,6)\)
- A point directly below it: \((3,2 - 4) = (3, -2)\)
- A point directly to the right: \((3 + 4,2) = (7,2)\)
- A point directly to the left: \((3 - 4, 2) = (-1,2)\)
Using the Computer to Plot a Circle
On-line graphing calculators will often let you just enter the equation of the circle in any form you like, so this is much easier than drawing it by hand. However, there are some that insist on having an equation of the form \(y = \text{something}\). Because our circle involves a term in \(y^2\), this means that we need to come up with two equations: one for each half (top and bottom) of the circle.
Example
Find equations that will let you plot the circle \((x - 3)^2 + (y - 2 )^2 = 16\) using an archaic on-line graphing calculator that insists on having equations of the form \(y = \text{something}\).
Solution:
This circle has centre \((3,2)\) and radius \(\sqrt{16} = 4\). Rearrange the equation to make \(y\) the subject:
- \(y = 2 + \sqrt{16 - (x - 3)^2}\) and
- \(y = 2 - \sqrt{16 - (x - 3)^2}\)
That was a bit of a pain, wasn't it? If you find a graphing calculator that insists on doing this, I'd suggest you look around for one that will let you do it all in one go.
Description
A coordinate geometry is a branch of geometry where the position of the points on the plane is defined with the help of an ordered pair of numbers also known as coordinates. In this tutorial series, you will learn about vast range of topics such as Cartesian Coordinates, Midpoint of a Line Segment etc
Audience
year 10 or higher, several chapters suitable for Year 8+ students.
Learning Objectives
Explore topics related to Coordinates Geometry
Author: Subject Coach
Added on: 27th Sep 2018
You must be logged in as Student to ask a Question.
None just yet!