The Set of All Points That ... (Locus)

A set is a collection of objects that have some property in common.

Mathematicians often talk about the set of all points that have a certain property. The technical term for this is a Locus. The set of points satisfying a property often forms a line, a surface or a curve. We can then say that the locus is the path taken by a point that moves so that it satisfies the property.

Let's have a look at some examples.

A Straight Line

A straight line can be thought of as the set of all points that satisfy a certain equation, or the path taken by a point that moves so that it is the same distance from two other points. If we fill in a few of these points, then a few more, and then a few more, we start to see that the locus of these points is a straight line, as shown in the picture below:

A Circle

When you draw a circle with a pair of compasses, you set a radius, stick the end of your compasses into the paper, and swing your pencil around so that it traces out the set of all points that are a fixed distance (the radius) away from a fixed point (the centre) of the circle. So, the circle is an example of a locus as well. To confirm this, you could plot a number of points, and join them up to form the circle, as shown in the picture below:

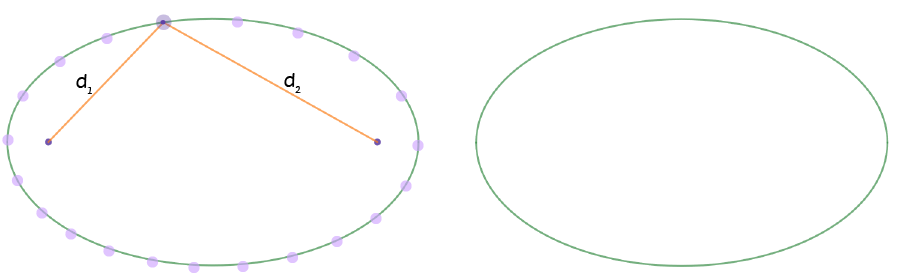
An Ellipse

An ellipse is a bit like a squashed circle. Instead of a fixed central point, we have two central points called foci. The ellipse is the locus of a point that moves so that its distances from two fixed points, called the foci, add up to some fixed constant. No matter where a point is on the ellipse, the distances \(d_1\) of the point from the first focus and \(d_2\) from the second focus add up to give a constant:

To confirm this, you could plot a number of points, and join them up to form the ellipse, as shown in the picture below:

A Parabola

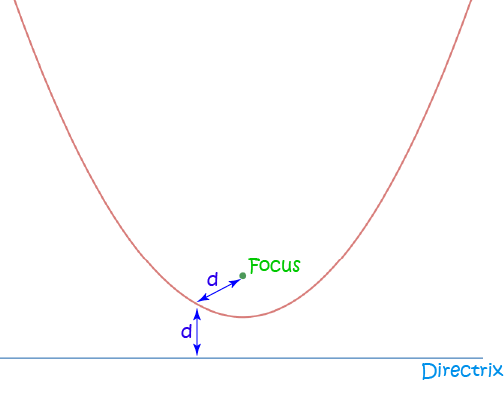
A parabola, e.g. the graph of \(y = x^2\) is an example of a locus too. It is the locus of a point that moves so that its distance from a fixed point, called the focus, is equal to its distance from a fixed line, called the directrix, as shown in the picture below:

In 3-Dimensional Space

Can we talk about a locus in 3-D space as well? Of course we can. We can come up with all sorts of weird and wonderful surfaces. Here are a few examples:

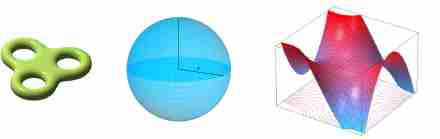
The middle one is a sphere, of course. Its description as a locus is easy to understand: like the circle, it is the locus of a point that moves so that its distance from a fixed point, called the centre is equal to a fixed constant, called the radius. The others can be described as sets of points as well, but their descriptions are a bit too complicated to give in this article.