Equation of a Straight Line From Two Points

A Little Bit of Nonsense

Actually, there's another version of the equation of a straight line that can help Edward out (and, being stubborn, I claim that you don't need it. More of that later!).

Deriving the Equation of a Line from Two Points

We've already seen the point-gradient equation for a straight line. In case you've forgotten, it's:

But what if we only know the two points \((x_1,y_1)\) and \((x_2,y_2)\), and not the gradient of the line? Well, we can work out what the gradient is, and then we'll have all the information we need to find the equation of the line. Let's hop to it (do echidnas hop? Maybe "scurry" is a better word.): It looks like our two points give us all the information we need to find the point-gradient equation of the line: So the equation we're after is

I hope someone is screaming that I could have just divided by zero. They'd be absolutely correct, but if \(y_2 - y_1 = 0\), then \(y_2 = y_1\) and our line must be vertical. We already know that the gradient of a vertical line is undefined, and we need to come up with a more cunning plan to write down its equation. So, everything is fine. This is the equation for a line that is not vertical and passes through the two points \((x_1,y_1)\) and \((x_2,y_2)\).

Before we apply our equation to Edward's termite mound, let's have a look at a few examples.

Example 1

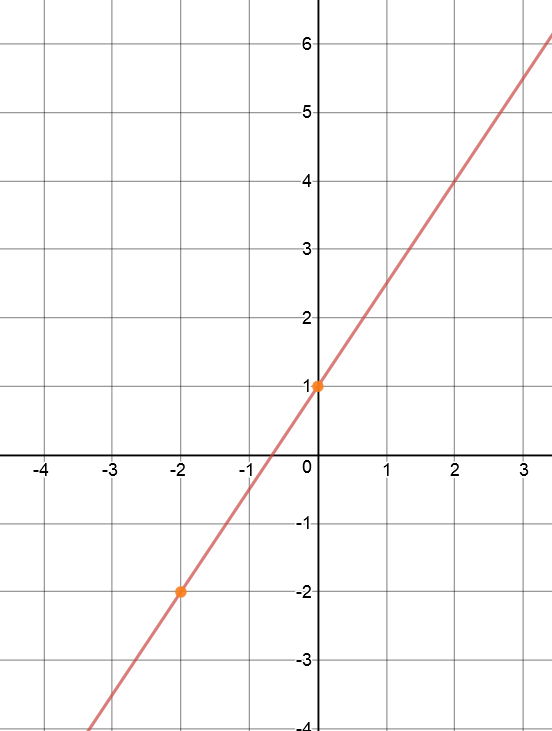
Find the equation of the line through the points \((0,1)\) and \((-2, -2)\).

Solution:

Set \((x_1,y_1) = (0,1)\) and \((x_2,y_2) = (-2,-2)\). Then

So the graph looks like this:

Example 2

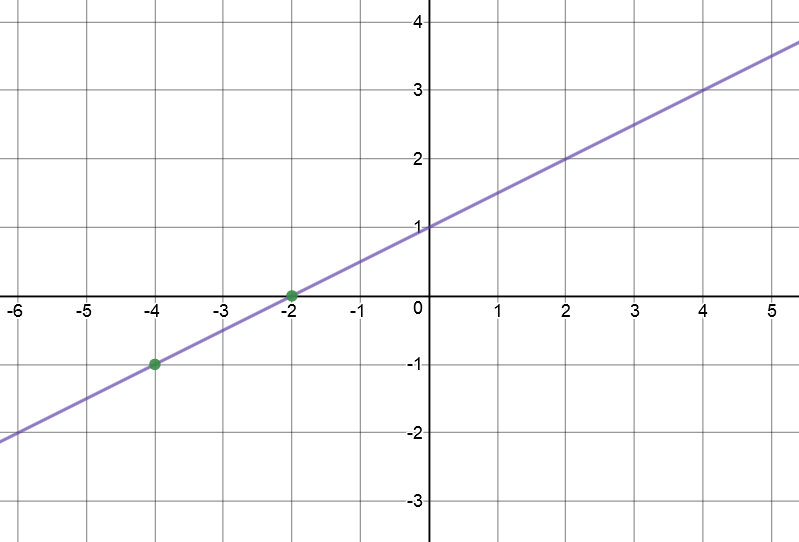
Find the equation of the line through the points \((-4,-1)\) and \((-2, 0)\).

Solution:

Set \((x_1,y_1) = (-4,-1)\) and \((x_2,y_2) = (-2,0)\). Then

So the graph looks like this:

Example 3

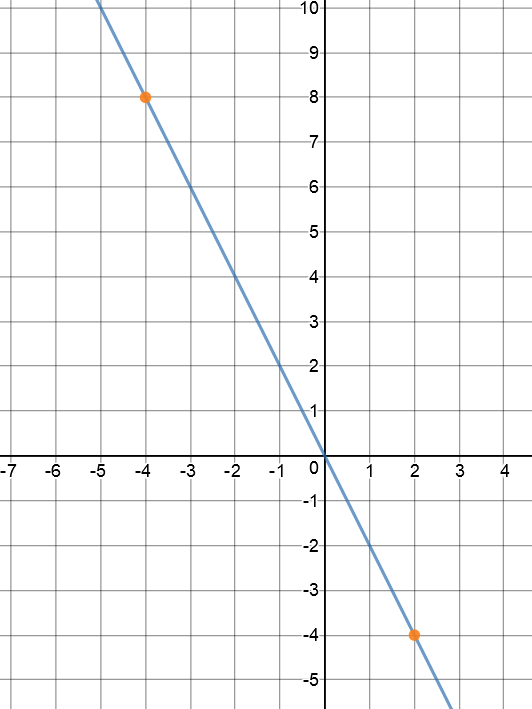
Find the equation of the line through the points \((2,-4)\) and \((-4, 8)\).

Solution:

Set \((x_1,y_1) = (2,-4)\) and \((x_2,y_2) = (-4,8)\). Then

So the graph looks like this:

Now It's Time to Solve Edward's Problem

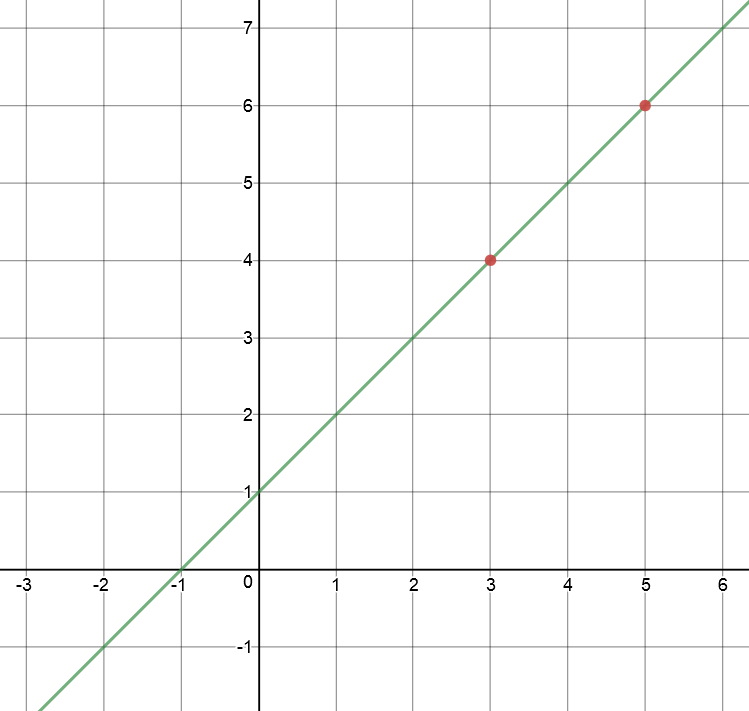
Do you remember that Edward wanted to find the height of his termite hill when its base radius measured 20 snouts? He knew that the height was 4 snouts when the base radius was 3 snouts and the height was 6 snouts when the base radius was 5 snouts. The height grew linearly with respect to the base radius, so he was looking for the equation of a straight line through the points \((3,4)\) and \((5,6)\). Using our new formula, and setting \((\text{radius}_1,\text{height}_1) = (3,4)\) and \((\text{radius}_2,\text{height}_2) = (5,6)\), we obtain

So the graph looks like this: and to find the height of the termite mound when the base radius is 20 snouts, we plug in \(\text{radius} = 20\) to give So, Edward's termite mound will be \(21\) snouts high.

The Alternative Approach

I'm allergic to memorising too many formulas, and I think that it's enough to memorise \(y = mx + b\) as the equation of a straight line.

Here's what I do:

1. Plug the two points into the equation \(y = mx + b\) individually, to give two equations in \(m\) and \(b\).
2. Solve the two equations simultaneously to find \(m\) and \(b\).
3. Write down the equation of the line in the form \(y = mx + b\).

Let's look at an example. It's just Edward's problem rephrased.

Example 5

Find the equation of the line through the points \((3,4)\) and \((5,6)\).

Solution:

1. Plug the two points into the equation \(y = mx + b\) individually, to give two equations in \(m\) and \(b\).
   • \((3,4)\) : \(y = 4\) and \(x = 3\), so \(4 = 3m + b\)
   • \((5,6)\) : \(y = 6\) and \(x = 5\), \(6 = 5m + b\)
2. Solve the two equations simultaneously to find \(m\) and \(b\).
   Subtracting the second equation from the first yields

   \(\begin{align*} 6 - 4 &= (5 - 3)m + (b - b)\\ 2 &= 2m\\ 1 &= m \end{align*} \)

   Now plug \(m = 1\) into the first equation to find \(b\):

   \(\begin{align*} 4 &= 3(1) + b\\ 4&= 3 + b\\ 1 &= b \end{align*} \)
3. Write down the equation of the line in the form \(y = mx + b\).
   \(\begin{align*} y &= mx + b\\ y &= x + 1 \end{align*} \) So, the equation is \(y = x + 1\), which is exactly what we got using the other approach.

   I'll leave it to you to choose the approach you wish to follow. In another article we'll show how to find the equation of a line through two points using the point-gradient formula.