Math Definitions - Letter I
Chapters
Irrational Number
Definition of Irrational Number
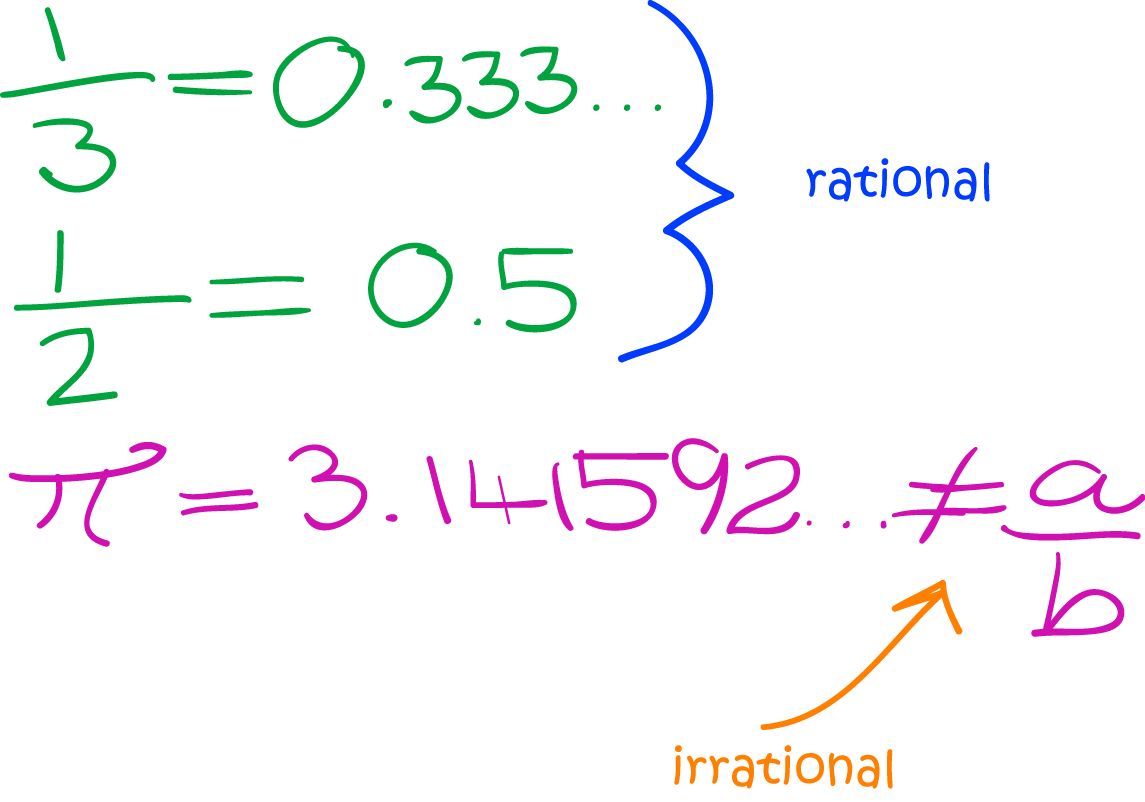
An irrational number is a number that cannot be written as a terminating or repeating decimal.
In other words, an irrational number is a number that can't be written as \(\dfrac{a}{b}\) for some integers, \(a\) and \(b\).
For example, \(\pi\) is an irrational number. Its digits are \(3.141592\dots\). They go on forever, but don't form any pattern that repeats.
Some other examples of irrational numbers are \(\sqrt{2}\) and Euler's number, \(e = 2.71828\dots\).
Description
The aim of this dictionary is to provide definitions to common mathematical terms. Students learn a new math skill every week at school, sometimes just before they start a new skill, if they want to look at what a specific term means, this is where this dictionary will become handy and a go-to guide for a student.
Audience
Year 1 to Year 12 students
Learning Objectives
Learn common math terms starting with letter I
Author: Subject Coach
Added on: 6th Feb 2018
You must be logged in as Student to ask a Question.
None just yet!