Univariate and Bivariate Data

Data sets can examine different numbers of variables. Univariate data is data related to a single variable. Bivariate data is data related to two variables.

Univariate Data

Some examples of data that involves only a single variable are

What Can You Do with Univariate Data?

We can analyse univariate data in ways that help us to describe our data set. This can include:

• Exploring central values of the data using measures such as the mean (average), median (middle value) and mode (most common value).
• Examining the spread of the data using measures such as the maximum and minimum values, range, variance, standard deviation and interquartile range.
• Plot the data on bar charts, pie charts or histograms. Note that these all plot the frequencies of the values of a single variable.

A question you might seek to answer with univariate data is "How many of the flowers in my garden have more than 6 petals?"

Bivariate Data

Bivariate data has two variables. To form bivariate data, we collect two different types of data. We collect bivariate data when we want to examine the relationships between things, or to decide whether one variable may have caused the other.

Example: Pet Food

Here is the data that I've collected so far:

and here is a scatter plot of this data: It looks like heavier dogs take less time to get through their food, but the relationship is not perfect. I can see this even more clearly, if I draw a line of best fit:

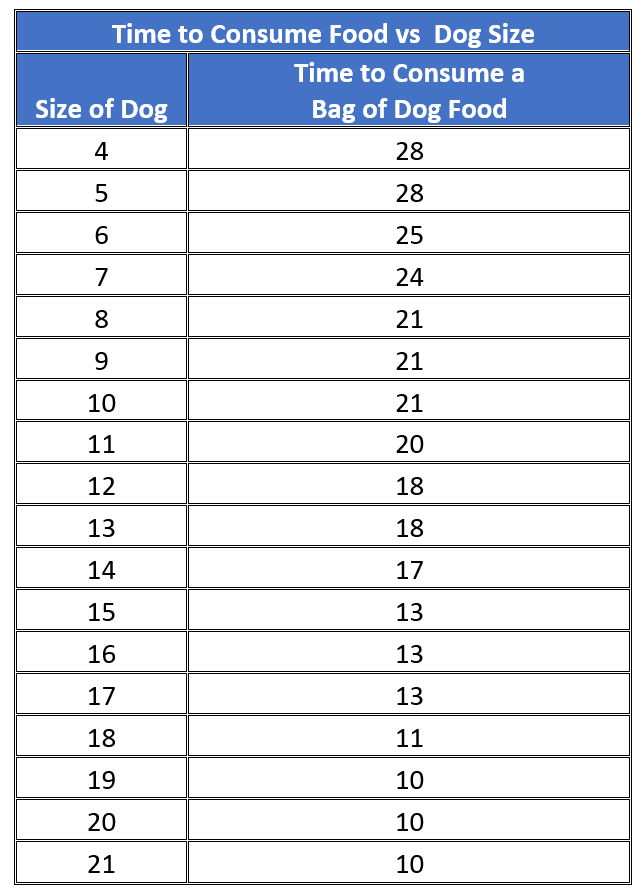
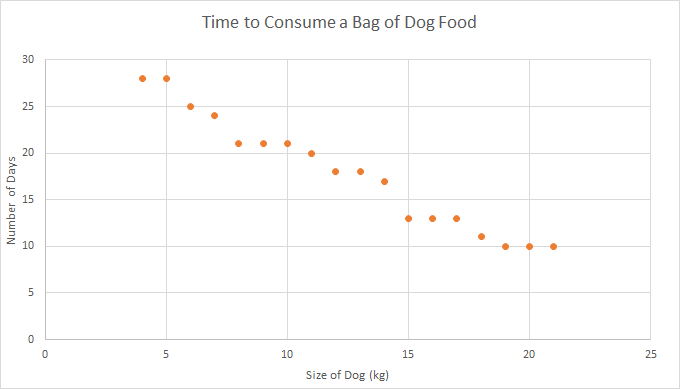
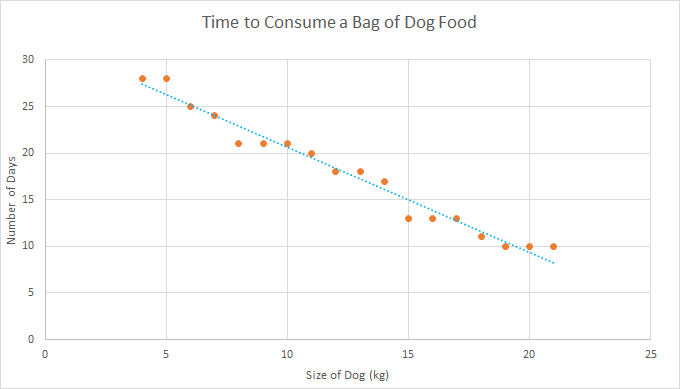
So, in summary, we use bivariate data when we want to examine the relationships between two variables, or the causes for things.

Using Bivariate Data

We analyse bivariate data to help us explain these relationships. Our analysis might include:

• Comparing the central measures and spread of the two variables when considered individually: mean, median and mode, maximum, minimum, range, variance, standard deviation, interquartile range, etc.
• Looking for correlations between the data.
• Looking for relationships, causes and explanations.
• Drawing up side by side tables of the two variables to lay the data out for comparison.
• Identifying independent and dependent variables.
• Drawing scatter plots and line graphs, and plotting lines of best fit.

A question you might seek to answer using bivariate data would be, "Is there a relationship between the size of a flower and the number of petals it has?"