Finding the Mean

The mean is just a fancy word for the average of a list of data values. To find the mean of a list of data values:

1. Add up all the numbers in the list.
2. Divide by the number of elements in the list.

Example 1

Find the mean of the list

Solution:

Start by adding these numbers:

Now divide this sum by the number of elements in the list. As there are \(6\) elements in the list, the mean is \(\dfrac{42}{6} = 7\).

What Are We Doing When We Find the Mean?

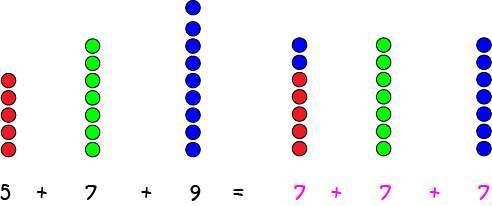
Essentially, we're evening the scores in the list out. If all the scores in the list were the same, and added to the same sum, they would all be equal to the mean. In other words, we shift parts of the numbers in the list around to make them all the same, just like in this picture:

The mean of the list \(\{5,7,9\}\) is equal to \(7\). The total \(5 + 7 +9 \) is the same as the total obtained by adding three copies of the mean value.

Example 2

Find the mean of the list

Solution: Start by adding these scores. Their sum is:

Now count the values: there are 17 numbers in this list. The mean is equal to the sum of the values divided by the number of values, which is \(\dfrac{349}{17} = 20.529\dots\).

What About Lists With Negative Values?

Just add them as before. Remember that \(2 + (-1) = 2 - 1 = 1\). Let's look at an example.

Example 3

Find the mean of the following list of values:

Start by adding the values in the list:

Now divide by the number of elements in the list (\(5\)) to give the mean:

The mean of our list is \(5\).

Let's finish with one last example that sends the cuteness rating for this article off the scale. I just adore golden retriever puppies (yes, Lucy, I love my Cavalier puppy too!).

Example 4

Conclusion

Now it's time to get lots of practice at finding the means of lists of data. For example, you could calculate the mean weight of the apples in the fruit bowl, or the mean diameter of the brussels sprouts you are served up for dinner. What else would you do with them? Don't forget to thank your parents for their help with your maths!