Data
Chapters
Explaining Quincunx
Explaining Quincunx

Sir Francis Galton (1822-1911) was an English statistician who invented a machine called a quincunx in 1873 to demonstrate the links
between some probability distributions and the normal distribution. Some other names for the quincunx include the Galton Board, Bean Machine
and Plinko.
The University of Colorado at Boulder has developed an online simulation of a quincunx machine that is fun to play with. You can have a play yourself at plinko. If you want to change the probability that the balls go to either side, go to the lab setting and see the effects of changing the numbers of rows and changing the probability of balls landing on the right or left. A few screen shots from this simulation are shown below to give you the idea.
A quincunx board is an array of pegs. Balls are released from a bucket at the top, and bounce onto the top peg, and then down the rows of pegs, eventually landing in one of a row of bins at the bottom of the board. Balls can bounce to the left or the right after they hit each peg.
Equal Probability of Going to the Right or Left
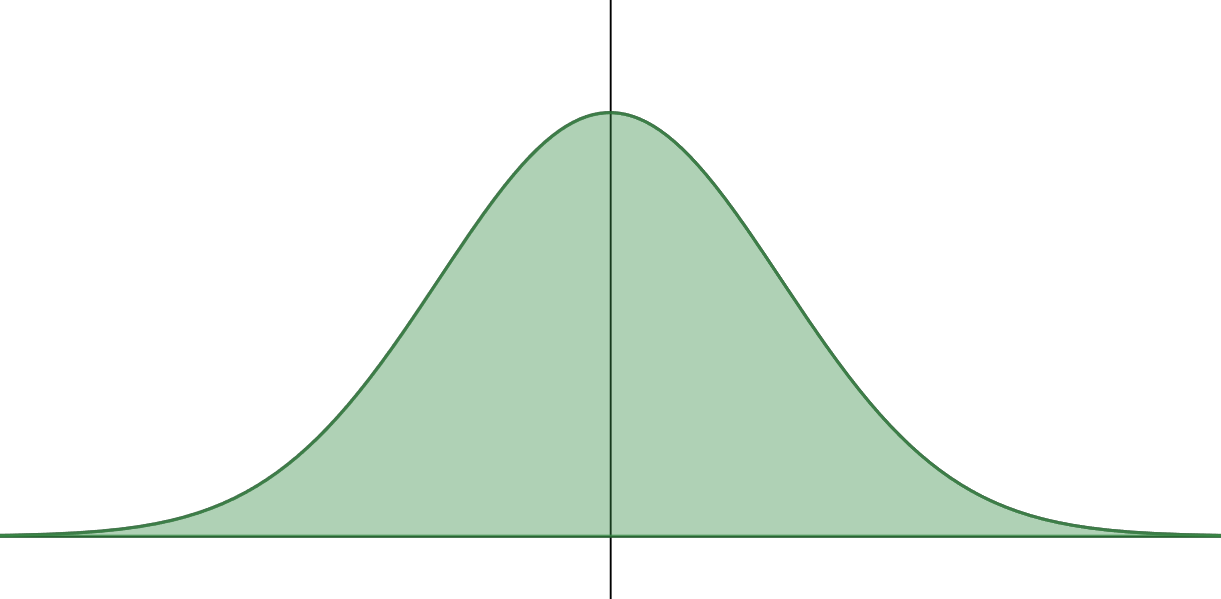
When balls have an equal probability of bouncing to the left or to the right from each peg, the collection of balls in the bins at the bottom of the quincunx board is shaped like a normal curve.
This is a screenshot of the standard simulation on the University of Colorado at Boulder's PhET Interactive Simulations site. The balls have an equal probability of going to the left or the right of each pin. Can you see how the final landing pattern is quite symmetric around the middle pin and looks very like a normal curve?

When the probabilities of bouncing to the left and the right are not equal, the balls in the bins at the bottom of the board form a "skewed" normal distribution.
Calculating the Probabilities
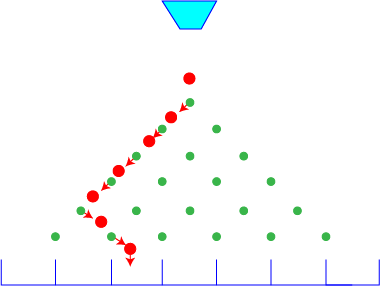
It is possible to calculate the probability of a ball landing in a particular bin.
Suppose we want to know the probability of a ball landing in the second bin from the left-most bin after bouncing through a 6 row quincunx board.
If the probability of bouncing to the right on every pin is \(p\), the probability of bouncing to the left on every pin is \(1 - p\). Let's start by calculating the probability that our ball takes the path shown in the picture to the 2nd bin from the left-most bin.
- It bounces to the left 4 times, with probability \((1-p)^4\)
- and then to the right twice, with probability \(p^2\)
To make life simpler, I'll number the bins from the left from now on, starting with bin 0 as the leftmost bin. We need to find the number of different paths that the ball can follow to bin number 2 (it always has to bounce 4 times to the left and 2 times to the right). There are two (equivalent) ways to do this:
- List all the paths like LLLLRR, LLLRRL, LLLRLR, etc and count them.
- Use combinations: we need the number of ways of choosing 2 right bounces from a collection of 6 bounces, or \(\begin{pmatrix}6\\2\end{pmatrix} = \dfrac{6!}{2!(6-2)!} = 15\).
This gives a total probability of landing in bin number 2 of \(15 (1-p)^4 p^2\). If \(p = 0.5\) (i.e. there's an equal chance of bouncing to the left or to the right), then the probability of landing in bin number 2 is 0.234375.
In general, suppose
- The quincunx has \(n\) rows.
- The probability of bouncing to the right is \(p\), and the probability of bouncing to the left is \(1 - p\).
The above formula is a bit confusing, but just remember: to land in the left-most bin, the ball needs to make no bounces to the right. To land in bin number 1, it needs to make \(1\) bounce to the right, etc. So, to land in bin number k, it needs to make \(k\) bounces to the right.
This formula is the formula for the binomial probability distribution. You can read more about it in the article on binomial probabilities.
Let's finish by calculating the probabilities for landing in each bin of a quincunx with 6 rows, for various values of \(p\).
\(p = 0.5\)
| Bin Number | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Probability | 0.015625 | 0.09375 | 0.234375 | 0.3125 | 0.234375 | 0.09375 | 0.015625 |
\(p = 0.75\)
| Bin Number | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| Probability | 0.177978515625 | 0.35595703125 | 0.296630859375 | 0.1318359375 | 0.032958984375 | 0.00439453125 | 0.000244140625 |
Description
This chapter series is on Data and is suitable for Year 10 or higher students, topics include
- Accuracy and Precision
- Calculating Means From Frequency Tables
- Correlation
- Cumulative Tables and Graphs
- Discrete and Continuous Data
- Finding the Mean
- Finding the Median
- FindingtheMode
- Formulas for Standard Deviation
- Grouped Frequency Distribution
- Normal Distribution
- Outliers
- Quartiles
- Quincunx
- Quincunx Explained
- Range (Statistics)
- Skewed Data
- Standard Deviation and Variance
- Standard Normal Table
- Univariate and Bivariate Data
- What is Data
Audience
Year 10 or higher students, some chapters suitable for students in Year 8 or higher
Learning Objectives
Learn about topics related to "Data"
Author: Subject Coach
Added on: 28th Sep 2018
You must be logged in as Student to ask a Question.
None just yet!