Year 10+ Constructions
Chapters
Using a Straight Edge and Compass to Copy an Angle
Using a Straight Edge and Compass to Copy an Angle
Compass and straight edge constructions are of interest to mathematicians, not only in the field of geometry, but also in algebra. Ancient Greek mathematicians were interested in the problem of "trisecting an angle" (splitting an arbitrary angle into three equal parts) using only a straight edge and compass. It turns out that some, but not all angles can be trisected, but no-one managed to prove that some angles could not be trisected using a straight edge and compass until the 19th Century!
However, it is possible to copy an arbitrary angle using only a straight edge and compass.
For this construction, you will need a straight edge (ruler - but you won't be measuring anything), pair of compasses, a pencil and paper. I have drawn the pictures using the robocompass app. It's fun to play with, and you can use it to do all sorts of geometric constructions. There's a little bit of coding to learn, but a list of instructions is provided. Once you've written your little program, you can invite a few friends over, get out the popcorn, sit back, relax and enjoy the show. Be warned that, when you are using it to draw arcs, the robocompass compass point may appear to be a little away from the centre, but the drawing is actually accurate.The Construction
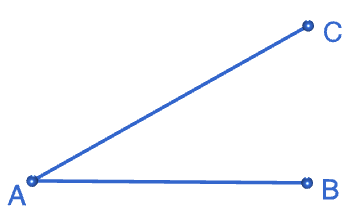
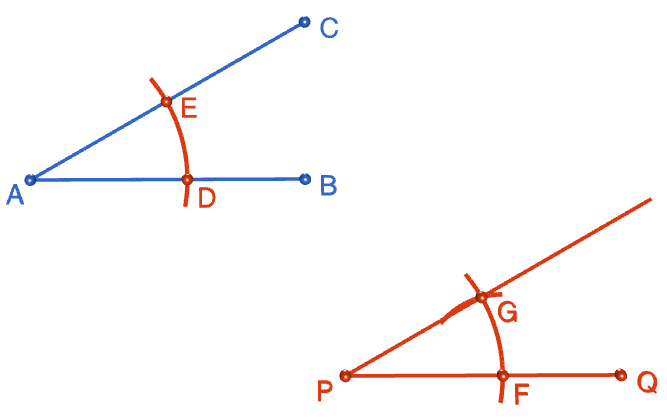
Step 1: Start out by drawing the angle \(CAB\) that you want to copy. Please don't be like Sam! Use a ruler to draw this.
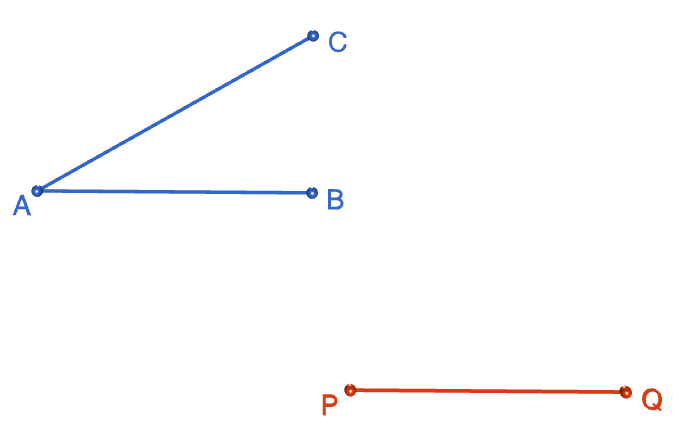
Step 2: Mark a point \(P\) away from your angle, and use it as the starting point to draw a line segment, \(PQ\). This line segment can go in any direction. It doesn't have to be parallel to either arm of the original angle, and it doesn't have to have the same length as either arm of the original angle. Just draw your favourite line segment of your favourite length and in your favourite direction (please use a straight edge).
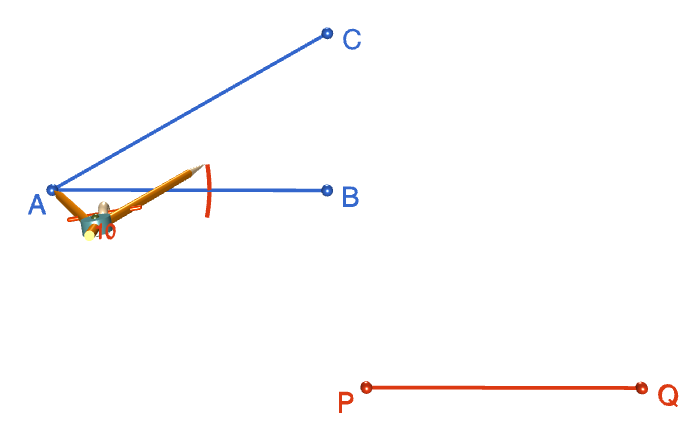
Step 3: Place the tip of your compasses on the point \(A\), and open them out to your favourite width. Draw an arc that cuts both arms of the angle. Mark the points where the arc cuts the arms of the angle with a \(D\) and an \(E\).
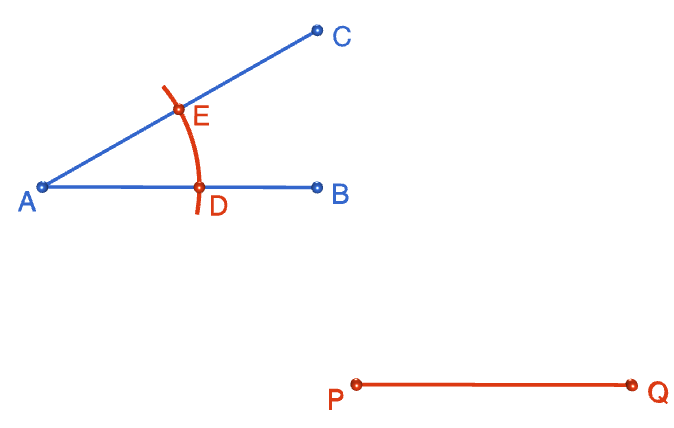
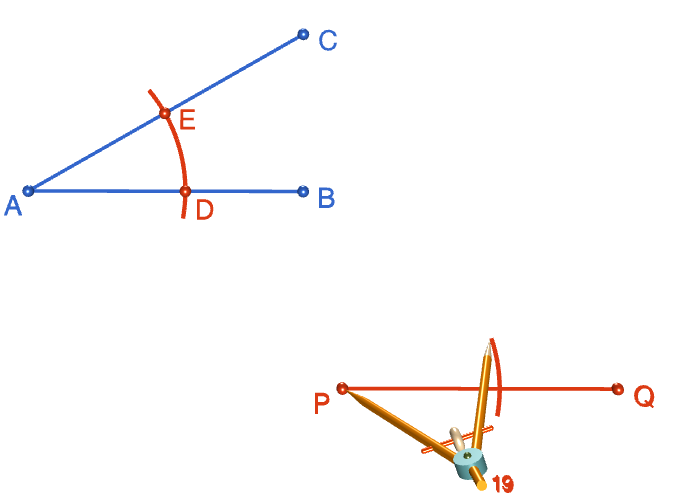
Step 4: Keeping your compasses at the same radius as in the preceding step, place the tip of your pair of compasses on the point \(P\). Draw an arc that looks like the one you drew across angle \(BAC\). Mark the point where the arc crosses the line segment \(PQ\) with an \(F\).
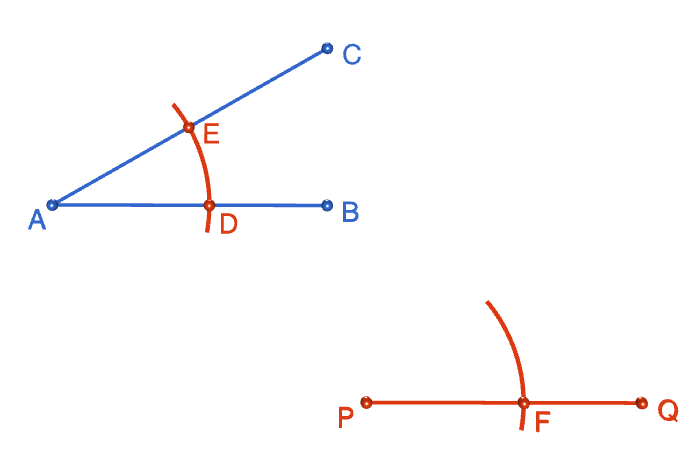
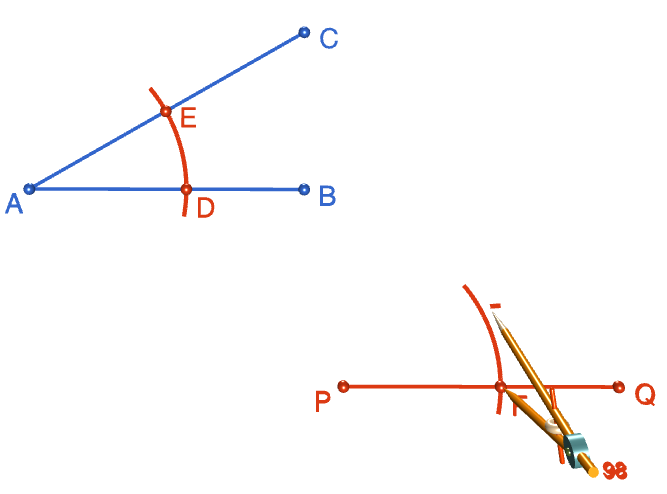
Step 5: Set the radius of your compasses to the distance between points \(D\) and \(E\). Keeping this radius fixed, move the tip of your compass down to point \(F\) and draw an arc, centred at point \(F\), that crosses the first arc you drew across line segment \(PQ\). Mark the point where the two arcs intersect with a \(G\).
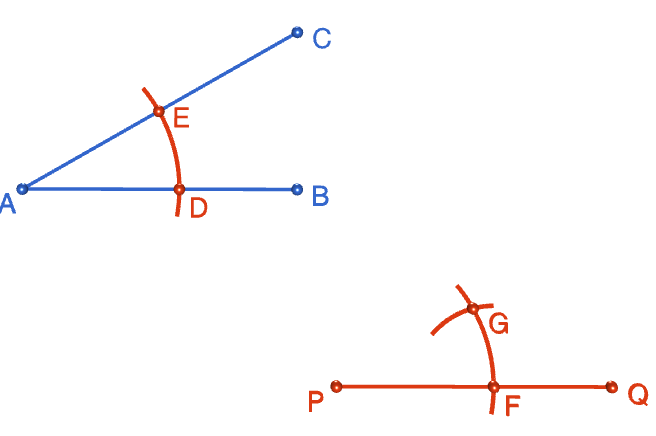
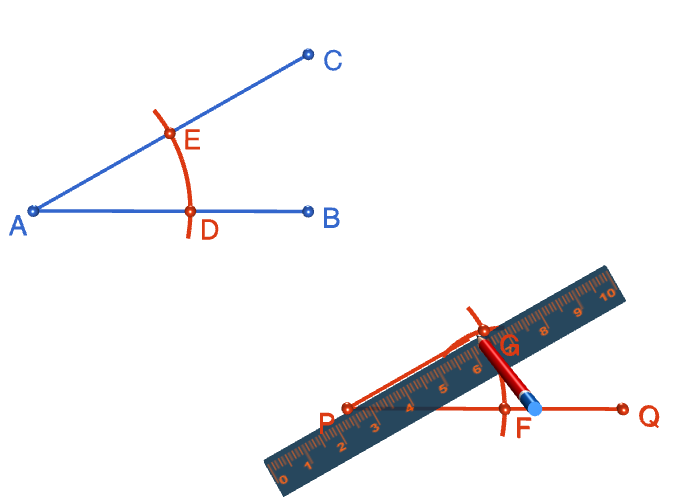
Step 6: Pull out your straight edge and draw the second arm of the new angle, starting at point \(P\) and passing through point \(G\). Make it as long as you like, and label the end point with an \(R\). Your new angle \(RPQ\) should be an exact copy of angle \(CAB\). Put your completed construction upper on the fridge with your other masterpieces.
Description
This tutorial will expose you to Rulers and how to use them. We will also have a close look as set square and compass constructions. Your feedback is important to us, if you like any other topic covered under this tutorial, please do let us know.
Audience
Year 10 or higher
Learning Objectives
Ruler and compass constructions and more
Author: Subject Coach
Added on: 27th Sep 2018
You must be logged in as Student to ask a Question.
None just yet!