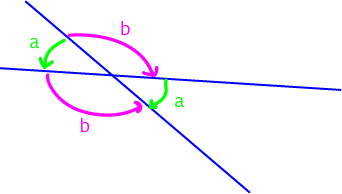
When two lines cross, they form four different angles. These four angles can be grouped into two pairs of vertically opposite angles. One of these pairs is marked by green arrows (and the letter a) in the diagram, and the other is marked by pink arrows and the letter b. You can easily see why these angles are considered to be "opposite" each other, but you're probably wondering why they are "vertically" opposite each other. "Vertical" means up and down, doesn't it? This is even more curious when you realise that American books call these pairs of angles "vertical angles", forgetting about the "opposite" altogether.

Of course, living in the Southern Hemisphere, we are all too aware that "upwards" is a matter of opinion! But this isn't the reason for this curious name. Can you see how each pair of angles meets at a common point (corner)? This common point is called a vertex, and it is this "vertex" that gives us the "vertically" part of the term. The two angles in each pair are vertically opposite because they are on opposite sides of the same vertex.

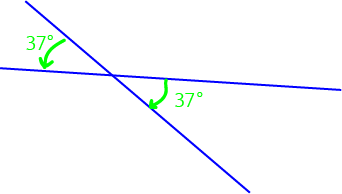
In the picture, the two angles marked with green arrows are vertically opposite angles. Since vertically opposite angles are equal, they both have the same size: \(37^\circ\).

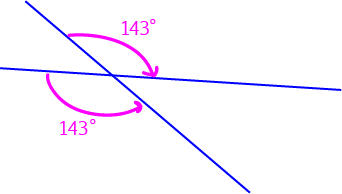
In the picture, the two angles marked with pink arrows are vertically opposite angles. Since vertically opposite angles are equal, they both have the same size: \(143^\circ\).

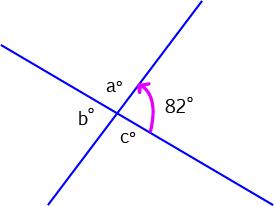
Exercise: Find all the unknown angles in the picture on the left.

Solution: First, the angle labelled with \(b^\circ\) is vertically opposite the angle labelled with \(82^\circ\). So, we must have \(b^\circ = 82^\circ\).

Now we need to work out the remaining angles. But remember that a straight angle is equal to \(180^\circ\). So, \(a^\circ + 82^\circ = 180^\circ\), and \(a^\circ = 180^\circ - 82^\circ = 98^\circ\).

Finally, \(c^\circ = a^\circ\) since they are vertically opposite angles. Therefore, \(c^\circ = 98^\circ\).

So, the answer is \(a^\circ = 98^\circ\), \(b^\circ = 82^\circ\) and \(c^\circ = 98^\circ\).