Parallel and Perpendicular Lines

Did you know that you could use algebra to decide whether a pair of lines was perpendicular or parallel? No, you don't just draw them and look, Al, we have to examine their equations. So, how do we tell?

The Gradient-Intercept Form of the Equation of a Straight Line

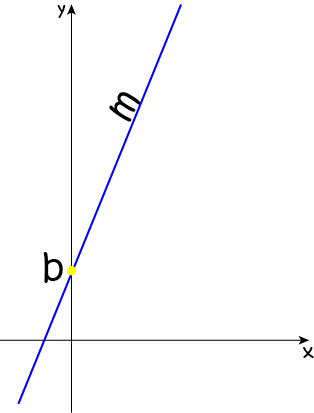
Do you remember this form of the equation of a straight line?

\(y = mx + b\)

Actually, it's the only one I ever use. I did memorise the other forms when I was at school, but now I always fall back on this one. There are two constants in this equation: \(m\), which represents the gradient (or slope) of the line, and \(b\), which tells us where the line cuts the \(y\)-axis. It's called the \(y\)-intercept. When we're trying to work out whether lines are parallel or perpendicular, we almost couldn't care less about the value of \(b\). The gradient (\(m\)) is the one we're interested in.

Parallel Lines

Two lines are parallel if their slopes are the same. In other words, the values of \(m\) in their gradient-intercept equations will be equal.

Let's try an example or two. This is a typical question from a maths text book.

Example

Alice the cow is plotting the growth of grass in her field. She observes that it has a height of \(y = 3x - 1\) centimetres, where \(x\) is the number of days since the grass seeds were planted. She knows that grass growth always follows a straight line equation, parallel to her own, and notices that the grass in a nearby field was \(1\) centimetre high \(1\) day after it was planted. Alice wants to find the equation for the growth of the grass in the nearby field.

Now, this is obviously an important real-world application of parallel straight lines. Your maths book would probably just ask you to find the equation of a straight line through the point \((1,1)\) that is parallel to the line \(y = 3x - 1\). How boring is that?

Either way, it's time to solve the problem.

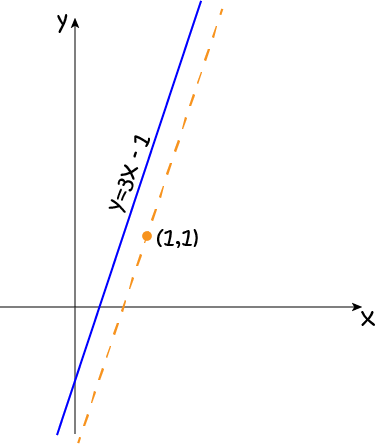
We know that, for two lines to be parallel, their slopes must be equal. The slope of a line is the number that multiplies the \(x\) in its equation. So, the slope of Alice's equation is \(3\). This means that the value of \(m\) for the equation for the nearby field will also be \(3\).

Here's what I'd do next:

The equation for the nearby field is \(y = 3x + b\), for some value of \(b\). I need to find the value of \(b\) that lets this line pass through the point \((1,1)\). I plug \(x = y = 1\) into this equation to give:

\( \begin{align*} 1 &= 3(1) + b\\ 1 &= 3 + b\\ -2 &= b \end{align*} \)

So, the equation for the nearby field is \(y = 3x - 2\). End of story!

Here's what your textbook will encourage you to do. The point-slope equation of a straight line looks like this:

\( (y - y_1) = m(x - x_1) \)

Our \(m\)-value must be \(3\). So, we have

\( (y - y_1) = 3(x - x_1) \)

and we want the line to pass through the point \((1,1)\), so we plug this in for \((x_1,y_1)\) to give

\( (y - 1) = 3(x - 1) \)

Oh, dear! This is in a different form from our original equation. We'll need to rearrange it into gradient-intercept form:

\( \begin{align*} (y - 1) &= 3(x - 1)\\ y - 1 &= 3x - 2\\ y &= 3x - 3 + 1\\ y &= 3x - 2 \end{align*} \)

So, the equation for the nearby field is \(y = 3x - 2\).

I'll leave you to choose your weapon for this problem. I've already chosen mine.

Make Sure it Isn't the Same Line

If two lines have the same slope there are two things that can happen:

• They are different, parallel lines.
• They are just different equations for the same straight line.

Just watch out for the second one. Sometimes questions try to trick you. Let's look at an example.

Example

Is the line \(y = 2x + 5\) parallel to the line \(y - 5 = 2x\)?

The slope of \(y = 2x + 5\) is \(2\), and its \(y\)-intercept is \(5\).

The slope of \(y - 5 = 2x\) is \(2\), and its \(y\)-intercept is also \(5\).

The only way two lines can have both the same slope and the same \(y\)-intercept is if they are the same straight line.

So, the answer is no. These lines are not parallel.

Note: This technique works for all straight lines except vertical ones. We'll see what to do with vertical lines later.

Perpendicular Lines

No, Al, this has nothing to do with the value of \(b\)!

We know that two lines are perpendicular if they intersect at a \(90^\circ\) angle to each other, but how do we work this out from their equations?

The answer is simple. We look at the gradients again. When we multiply the \(m\)-values together, we get \(-1\) for perpendicular lines:

Example

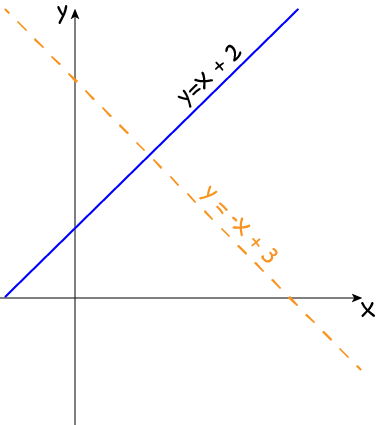
Are the lines \(y = x + 2\) and \(y = -x + 2\) perpendicular?

Yes! The slope of \(y = x + 2\) is \(1\), and the slope of \(y= -x + 2\) is \(-1\). \(1 \cdot (-1) = -1\), so the lines are perpendicular.

Note: Some people like to say this as "their slopes are negative reciprocals." If the slopes of the two lines are \(m_1\) and \(m_2\), this just says that

Example

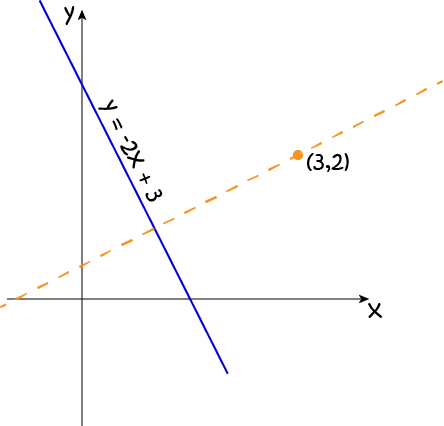
Find a line through the point \(3,2\) that is perpendicular to the line \(y = -2x + 3\).

The slope of the line \(y = -2x + 3\) is \(-2\), so the slope of our perpendicular line will be \(-\left(\dfrac{1}{-2}\right) = \dfrac{1}{2}\).

So, its equation has the form \(y = \dfrac{1}{2}\;x + b\).

Let's plug in the point \((3,2)\) to find \(b\):

\( \begin{align*} 2 &= \dfrac{1}{2}(3) + b\\ 2 &= 1.5 + b\\ 0.5 &= b \end{align*} \)

So, the equation is \(y = 0.5 x + 0.5\).

Alternatively, you can use the point-gradient form:

\( (y - 2) = \dfrac{1}{2} (x - 3) \)

and rearrange it to give \(y = 0.5x + 0.5\).

What About Those Pesky Vertical Lines?

Unfortunately, the gradient of a vertical line is undefined, so these tricks won't help you. We need to just remember that all vertical lines are parallel to each other, and that vertical and horizontal lines are perpendicular to each other.

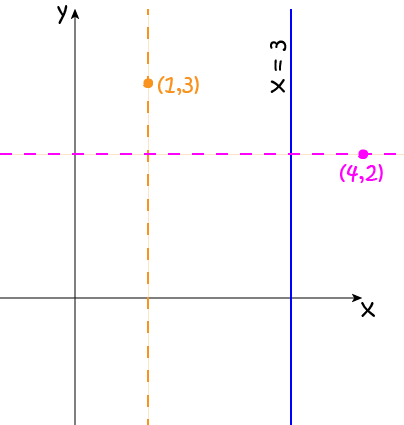
The line through the point \((1,3)\) that is parallel to the line \(x = 3\) is the line \(x = 1\).

The line through the point \(4,2\) that is perpendicular to the line \(x = 3\) is the line \(y = 2\).