Year 10+ Lines and Angles
Chapters
Parallel Lines and Pairs of Angles
Parallel Lines and Pairs of Angles
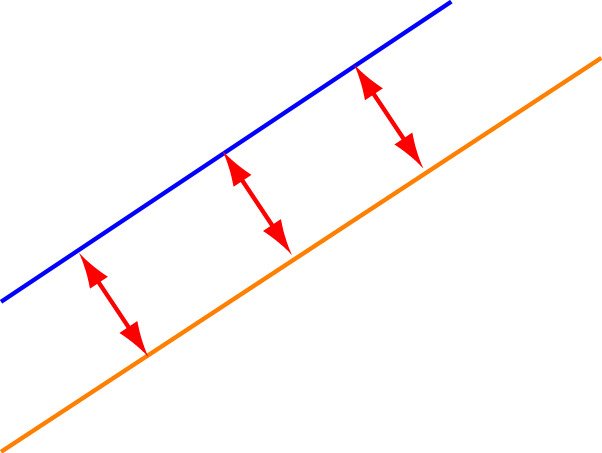
Two lines are parallel if they always stay the same distance apart and never cross each other.
In the examples below, the orange and blue lines are parallel

Example 1

Example 2
Pairs of Angles and Parallel Lines
A line that crosses two or more other lines is called a transversal. When a pair of parallel lines is crossed by a transversal, a number of different
pairs of angles are formed, many of which are equal, while others are supplementary (add to \(180^\circ\)). The diagrams below show these different angles.
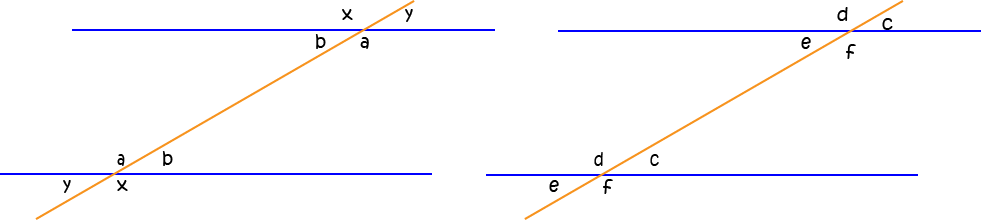
In the picture on the left, the blue lines are parallel and the orange line is a transversal. In addition:
- The pairs of angles labelled by \(a\) and \(b\) are
alternate angles - The pairs of angles labelled by \(x\) and \(y\) are
alternate exterior angles
In the picture on the right, the blue lines are parallel and the orange line is a transversal. In addition:
- The pairs of angles labelled by \(c\), \(d\), \(e\) and \(f\) are
corresponding angles - The pairs of angles labelled by \(c\) and \(f\), and \(d\) and \(e\) are
cointerior angles
Tests for Parallel Lines
Each type of angle pair gives rise to a test for parallel lines:
- If the two angles in any pair of alternate angles formed when a transversal cuts a pair of lines are equal, then the pair of lines is parallel
- If the two angles in any pair of corresponding angles formed when a transversal cuts a pair of lines are equal, then the pair of lines is parallel
- If the two angles in any pair of alternate exterior angles formed when a transversal cuts a pair of lines are equal, then the pair of lines is parallel
- If the two angles in any pair of cointerior angles formed when a transversal cuts a pair of lines are supplementary, then the pair of lines is parallel
So, if you have two lines cut by a transversal and you find a pair of alternate angles that are not equal, or a pair of alternate exterior angles that are not equal, or a pair of corresponding lines that are not equal, or a pair of cointerior angles that are not supplementary, then you know that the two lines are not parallel.
Let's look at some examples.
Examples
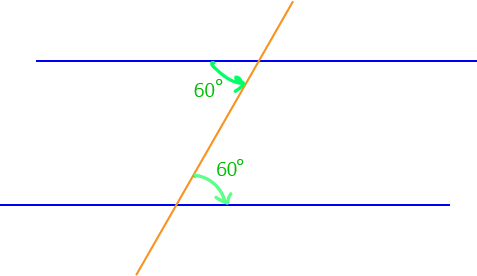
In the picture, both alternate angles marked in green are equal to \(60^\circ\). So, the two blue lines are parallel.
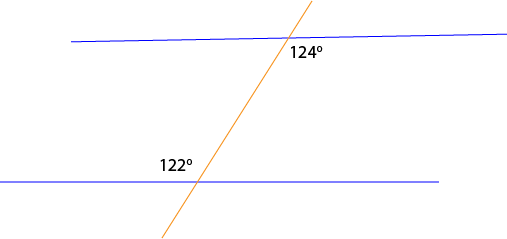
In the picture, one of the alternate angles is equal to \(124^\circ\), but the other is equal to \(122^\circ\). The two blue lines are not parallel.
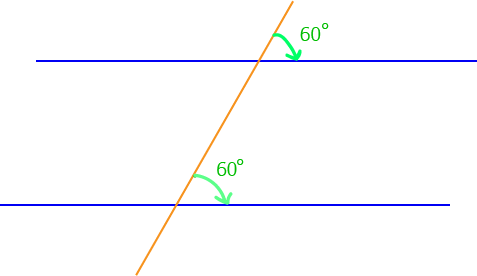
The picture shows a pair of corresponding angles that are equal (to \(60^\circ\)). Therefore, the two blue lines are parallel.
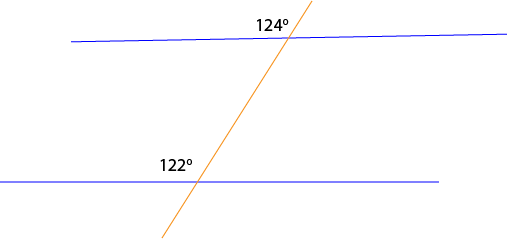
In the picture, one of the corresponding angles marked is \(124^\circ\), while the other is \(122^\circ\). As these corresponding angles are unequal, the two blue lines are not parallel.
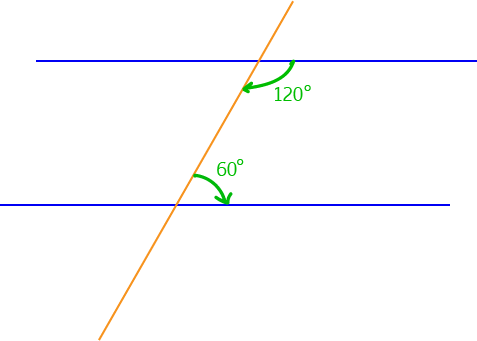
The picture shows a pair of cointerior angles that is supplementary (\(120^\circ + 60^\circ = 180^\circ\)). Therefore, the two blue lines are parallel.
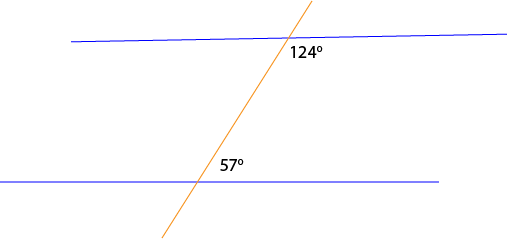
In the picture, the pair of cointerior angles adds up to \(57^\circ + 124^\circ = 181^\circ \neq 180^\circ\). As this pair of cointerior angles is not supplementary, the two blue lines are not parallel.
Description
In this mini book, you will learn about
- Alternate angles
- Cointerior angles
- Radians
- Vertically Opposite Angles
and several other topics related to lines and angles.
Audience
Year 10 or higher
Learning Objectives
To learn the basics of Lines and Angles stream of Geometry
Author: Subject Coach
Added on: 28th Sep 2018
You must be logged in as Student to ask a Question.
None just yet!