Year 10+ Lines and Angles
Chapters
Transversals
Transversals
A transversal is a line that intersects with two or more other lines.
In each of the examples below, the red line is a transversal. The lines cut by transversals need not be parallel, but they can be. Transversals can cut two, three, four, five, or as many lines as you like.
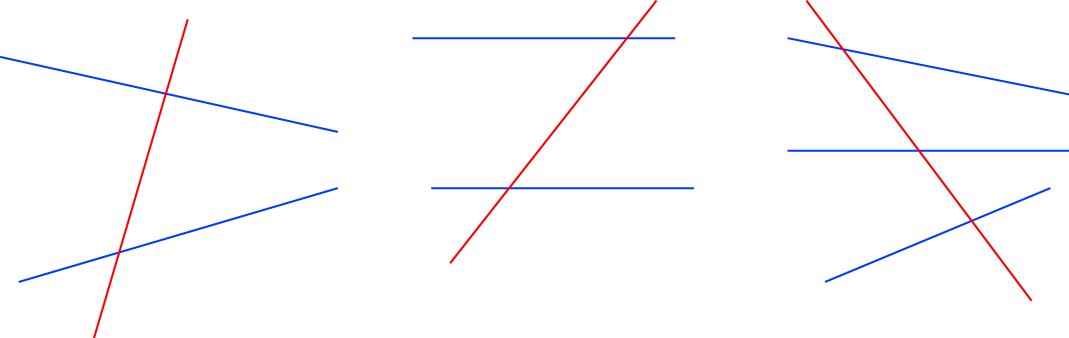
Transversals and Angles
When transversals cut lines, they form many different pairs of angles. There are four types of angles that we are particularly interested in when we do geometry, because these have special properties when the lines that have been cut by the transversal are parallel.
Alternate Angles
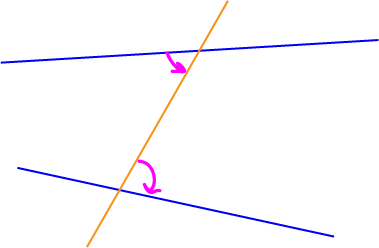
In the picture, the two lines are blue, and the transversal is orange. Alternate angles lie between the two lines, but on either side of the transversal. The picture shows one pair of alternate angles, marked by pink arrows, but there is another (take the two angles on the opposite side of the
transversal from the one in the picture). Can you see how they are the angles inside a "z"-shape? (the "z"-shape runs along the top blue line from left to right up to the transversal, down the transversal and then
to the right along the bottom blue line).
If the two blue lines were parallel, the alternate angles would be equal. As they aren't parallel, the only thing we can say is that the alternate angles are not equal.
Alternate Exterior Angles
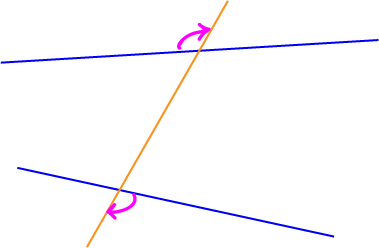
These are really just alternate angles, but this time, they're on the outsides of the two lines. In the picture, the two lines are blue, and the transversal is orange. Alternate exterior angles lie outside the two lines, but on either side of the transversal. The picture shows one pair of alternate angles, marked by pink arrows, but there is another (take the two angles on the opposite side of the
transversal from the one in the picture).
If the two blue lines were parallel, the alternate exterior angles would be equal. As they aren't parallel, the only thing we can say is that the alternate exterior angles are not equal.
Cointerior Angles
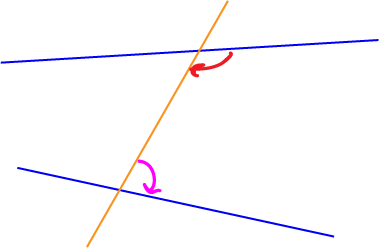
In the picture, the two lines are blue, and the transversal is orange. Cointerior angles lie on the same side of the transversal, in between the two lines. The picture shows a
pair of angles, marked with pink and red arrows. Those two angles are cointerior. There is another pair of cointerior angles in this picture. They lie on the opposite side of the transversal, between the two blue
lines. Do you see how cointerior angles are the angles inside a "C"-shape (or backwards "C"-shape)? The ends of the two blue lines heading from the right to the left form the top and bottom of the "C", and the transversal
forms the back of the "C".
If the two blue lines were parallel, each pair of cointerior angles would add up to \(180^\circ\). As they aren't parallel, the only thing we can say is that each pair of cointerior angles does not add up to \(180^\circ\).
Corresponding Angles
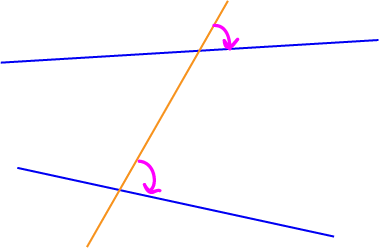
In the picture, the two lines are blue, and the transversal is orange. Corresponding angles lie on the same side of the transversal, and the same side of each of the lines (either both above or both below). The picture shows a
pair of angles, marked with pink arrows. Those two angles are corresponding angles. There are three other pairs of corresponding angles in this picture. One of them lies above the two lines, but on the other side of the transversal. See if you
can work out where the other two pairs are.
If the two blue lines were parallel, each pair of corresponding angles would be equal. As they aren't parallel, the only thing we can say is that each pair of corresponding angles is not equal.
Description
In this mini book, you will learn about
- Alternate angles
- Cointerior angles
- Radians
- Vertically Opposite Angles
and several other topics related to lines and angles.
Audience
Year 10 or higher
Learning Objectives
To learn the basics of Lines and Angles stream of Geometry
Author: Subject Coach
Added on: 28th Sep 2018
You must be logged in as Student to ask a Question.
None just yet!