Year 10+ Measurement
Chapters
The Metric System of Measurement
The Metric System of Measurement
In Australia and New Zealand, the official system of measurement used is the metric (or SI) system. It has seven basic units, but we can build most units of measurement out of the three units:
- \(m\): the metre for measuring length.
- \(kg\): the kilogram for measuring mass.
- \(s\): the second for measuring time.
Let's look at a few examples.
Example 1
Metres

This didgeridoo has a length of about one metre. My four year old cousin, Timmy, has a height of about one metre.

This tape measure can measure lengths of up to 5 metres.
Kilograms

This weight has a mass of one kilogram.

6 small apples weigh about one kilogram.
Seconds

The thinnest hand on this clock is the second hand. One second is the about the time it takes for you to say "one one thousand".
Larger or Smaller Measurements
The metric system includes about 20 prefixes that let us describe larger and smaller lengths (or other measurements). Here are some examples:
Example 1
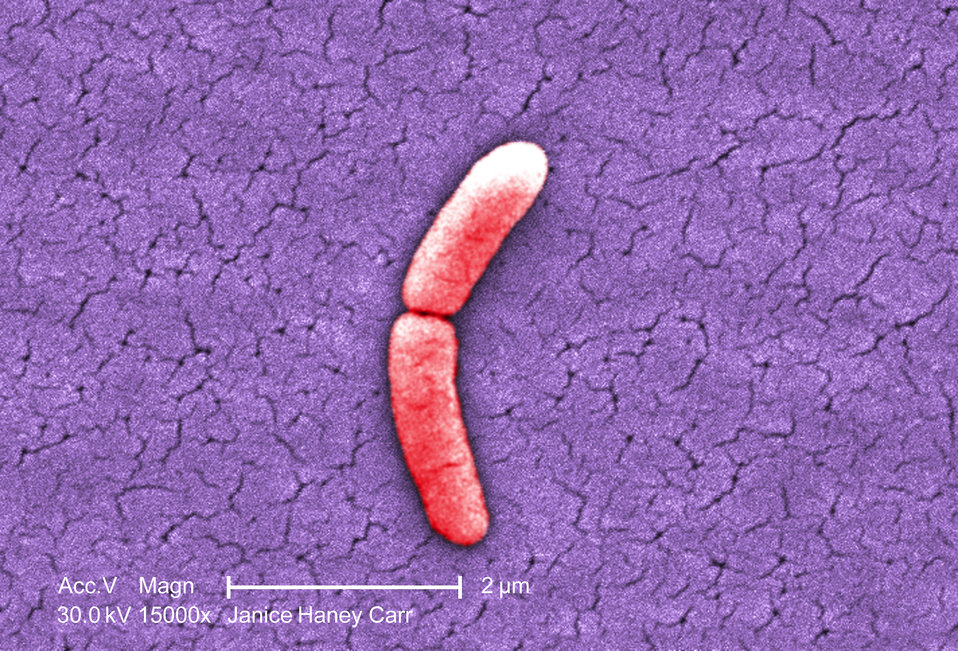
The picture on the left is a coloured electron micrograph of a Salmonella typhimurium bacterium that is undergoing cell division. You've probably heard of Salmonella: it's a nasty tummy bug that you can catch by eating contaminated food. The bacterium is impossible to see with the naked eye: this electron micrograph was taken using an electron microscope at a magnification of \(15,000 \times\). Each half of the bacterium measures \(0.000002\) m. I don't know about you, but I find it a bit tedious to have to write down all those zeroes all the time, and I can't really visualise what they mean. The metric system has found a way around this, by introducing the prefix micro, which corresponds to \(10^{-6}\). So, we could, more conveniently, write this length as \(2\) micrometres, or using the symbol \(2 \mu \text{m}\).
Example 2

While it might be OK to measure the distance that you walk on a track around a park in metres, it becomes very cumbersome to measure distances travelled on roads, such as the road from Sydney to Perth, in metres. Instead we use a larger unit called the kilometre. 1 kilometre is equal to 1,000 metres, and the prefix "kilo" means one thousand. The distance by road from Sydney to Perth is approximately 3,929.6 kilometres.
The Most Commonly Used Metric Prefixes
Name
Number
Prefix
Symbol
Trillionth
\(0.000000000001\)
pico
p
Billionth
\(0.000000001\)
nano
n
Millionth
\(0.000001\)
micro
\(\mu\)
Thousandth
\(0.001\)
milli
m
Hundredth
\(0.01\)
centi
c
Tenth
\(0.1\)
deci
d
Ten
\(10\)
deka
da
Hundred
\(100\)
hecto
h
Thousand
\(1,000\)
kilo
k
Million
\(1,000,000\)
mega
M
Billion
\(1,000,000,000\)
giga
G
Trillion
\(1,000,000,000,000\)
tera
T
| Name | Number | Prefix | Symbol |
|---|---|---|---|
| Trillionth | \(0.000000000001\) | pico | p |
| Billionth | \(0.000000001\) | nano | n |
| Millionth | \(0.000001\) | micro | \(\mu\) |
| Thousandth | \(0.001\) | milli | m |
| Hundredth | \(0.01\) | centi | c |
| Tenth | \(0.1\) | deci | d |
| Ten | \(10\) | deka | da |
| Hundred | \(100\) | hecto | h |
| Thousand | \(1,000\) | kilo | k |
| Million | \(1,000,000\) | mega | M |
| Billion | \(1,000,000,000\) | giga | G |
| Trillion | \(1,000,000,000,000\) | tera | T |
For example, your doctor might prescribe you a dose of medicine measured in milligrams (mg) or micrograms (\(\mu\)g). My computer has \(16\) gigabytes (Gb) of memory, and its hard drive holds \(1\) terabyte (Tb) of storage. If you buy sliced meat in Norway, it is sold by the hectogram (hg), and liquids are measured in decilitres (dl).
Why don't you try writing down the names and symbols for some units yourself? For example, what is the unit for one trillionth of a gram? How about a million litres?
Building Other Units
We can combine metres, kilograms and seconds to make new units of measurement. These units are referred to as derived units. Let's look at some of the common
derived units in the metric system.
Area
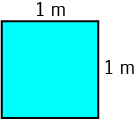
We can build area out of length. The area of a space is equal to a length times a length, so the basic unit of area is the area of a square that has side-lengths of 1 metre. The unit is \(\text{metres}\times \text{metres}\), written as \(\text{m}^2\), and said as "square metres".
Volume
Cubic Metres
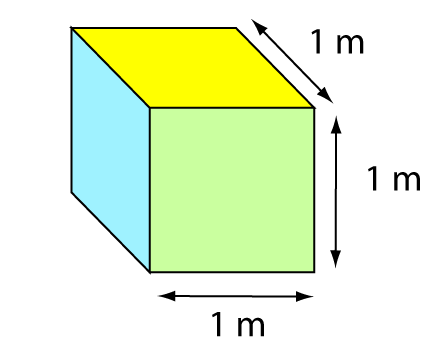
We can also build volume out of length. The volume of a space is equal to a length times a length times a length, so the basic unit of volume is the area of a cube that has side-lengths of 1 metre. The unit is \(\text{metres}\times \text{metres} \times \text{metres}\), written as \(\text{m}^3\), and said as "cubic metres".
Litres - Liquids

We tend to use the litre as the unit for measuring liquids (although they sell small vegetables by the litre at markets in Europe). The conversion is
The milk carton on the left contains 1 Litre of milk.
Time

It gets really cumbersome measuring times in seconds, so we have invented many larger units such as the minute (60 seconds), the hour (60 minutes), the day (24 hours), the week (7 days), and so on. If you tried to say that something was happening in 14 days using seconds, you'd have to say it would happen in 1,209,600 seconds, which wouldn't mean very much to anyone.
Speed
Speed is the distance that an object travels in a given period of time. We calculate it as \(\text{speed} = \dfrac{\text{distance travelled}}{\text{time taken}}\). Using the standard metric units for distance and time, this gives a unit of metres per second (abbreviated m/s) for speed. If something moves at 1 m/s, it travels 1 metre in every second.

It's more convenient to measure the speed of faster objects like this racing car, or an aeroplane in kilometres per hour (abbreviated km/h). We can convert kilometres per hour to metres per second as follows:
- There are 1,000 metres in a kilometre. So one kilometre per hour is 1,000 metres per hour.
- There are 3,600 seconds in one hour. So one kilometre per hour becomes \(\dfrac{1,000}{3,600} \approx 0.278\) metres per second.
Acceleration
Acceleration is the rate of change of the speed (or velocity) of an object.
When a cyclist accelerates from 5.5 m/s to 6.5 m/s, over a one second interval, they have accelerated at a rate of 1 metre per second per second. We abbreviate this unit as \(\text{m/s}^2\).
Force

A force is a push or a pull. The metric unit of force is the Newton (abbreviated N). A Newton is the amount of force required to make a 1 kg object accelerate at a rate of 1 \(\text{m/s}^2\). So, one Newton is equal to 1 kg \(\text{m/s}^2\). A Newton is derived from all three of the units: metre, kilogram and second.
The Rest of the SI Basic Units
The metric system was first implemented as the legal system of measurement in France in the 1800s. It has slowly been adopted as the universal system of measurements for scientists, and has been formalised under the name SI units (Système International d'Unités) since 1960. We need to add a few extra units to complete the list of base units for the SI system. The ampere is used to measure electric current, the mole is used to measure the amount of a substance, the candela is used to measure luminous intensity and the Kelvin is used to measure temperature. The complete list of SI base units is given in the table below.
| Quantity | Unit | Abbreviation |
|---|---|---|
| Time | second | s |
| Length | metre | m |
| Mass | kilogram | kg |
| Temperature | Kelvin | K |
| Electrical Current | Ampere | A |
| Amount of Substance | mole | mol |
| Luminous Intensity | candela | cd |
Description
In these chapters, you will learn more about measurement topics such as
- Metric numbers
- Speed
- Conversions
and several other topics
Audience
Year 10 or higher, some chapters are suitable for Year 8+ students
Learning Objectives
Learn about measurement and related topics
Author: Subject Coach
Added on: 28th Sep 2018
You must be logged in as Student to ask a Question.
None just yet!