Year 10+ Measurement
Chapters
Converting Areas
Converting Areas

Sam and Jasmin have decided that they'd like to build Christo a table for his model trains as a birthday present. They've designed the table top to have an area of \(2,040,000\) square millimetres and now they want to buy some artificial grass to cover it. But the artificial grass is sold by the square metre. So, Sam and Jasmin need to learn how to convert their measurements from square millimetres to square metres.
Learning to convert areas is a very useful skill, and one that we should all spend some time acquiring. In this article we'll look at how we can convert areas between various square units in the metric system. At the end, we'll talk about converting areas from metric units to Imperial units and vice versa.
Converting Metric Areas to other Metric Square Units
Square Centimetres to Square Millimetres and Back Again
Each centimetre is made up of \(10\) millimetres. So, a square with a \(1\) centimetre side length has a \(10\) millimetre side length. Because the area of a square is equal to its side-length squared, this means that \(1\) square centimetre is equal to \(10 \times 10 = 100 \) square millimetres as shown in the diagram below.
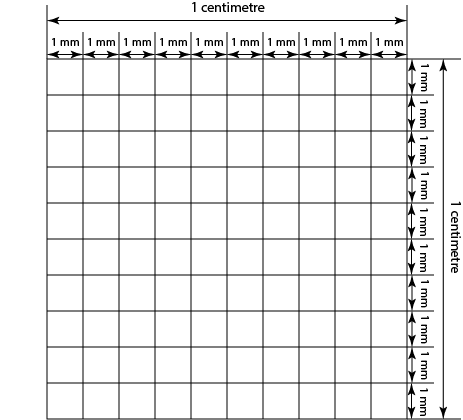
To convert an area from square centimetres to square millimetres, you need to multiply it by \(100\). For example, an area of \(23\) square centimetres would convert to \(23 \times 100 = 2,300\) square millimetres.
To convert an area from square millimetres to square centimetres, you need to remember that the square millimetre is the smaller unit, so you need to divide by \(100\). A measurement of \(366\) square millimetres would become \(366 \div 100 = 3.66\) square centimetres.
Square Metres to Square Centimetres and Back Again
Each metre is made up of \(100\) centimetres. So, a square with a \(1\) metre side length has a \(100\) centimetre side length. Because the area of a square is equal to its side-length squared, this means that \(1\) square metre is equal to \(100 \times 100 = 10,000 \) square centimetres. For example, a table top with an area of \(4\) square metres will have an area of \(4 \times 10,000 = 40,000\) square centimetres.
To convert an area from square centimetres to square metres, you need to remember that each square metre is made up of \(10,000\) square centimetres, so you need to divide your area by \(10,000\). For example, an area of \(40,000\) square centimetres would become an area of \(40,000 \div 10,000 = 4\) square metres.
Square Metres to Square Millimetres and Back Again
We know that there are \(100\) centimetres in a metre and \(10\) millimetres in a centimetre. Combining these two facts together tells us that there are \(1,000\) millimetres in a metre. So, a square with a side lenght of \(1\) metre has a side length of \(1,000\) millimetres. Because the area of a square is equal to its side-length squared, this means that \(1\) square metre is equal to \(1,000 \times 1,000 = 1,000,000 \) square millimetres.
To convert a measurement from square metres to square millimetres, simply multiply it by \(1,000,000\). For example, a table top with an area of \(3.5\) square metres has an area of \(3.5 \times 1,000,000 = 3,500,000\) square millimetres.
Sometimes, we need to convert areas in square millimetres to areas in square metres. To do this, remember that square millimetres are smaller than square metres and divide the number of square millimetres by \(1,000,000\). For example, the area of Sam and Jasmin's table top is \(2,040,000 \div 1,000,000 = 2.04\) square metres.
Square Metres to Hectares and Back Again
A hectare is a metric unit for area that is used to measure the areas of land and cities. \(1\) hectare (abbreviated as ha) is equal to the area of a square of side length \(100\) metres:
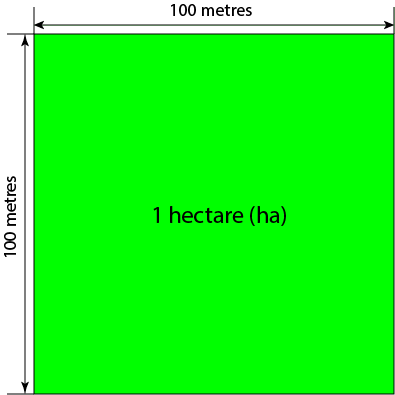
Since the area of a square is equal to its side-length squared, one hectare is equal to \(100 \times 100 = 10,000\) square metres.
To convert an area from hectares to square metres, simply multiply it by \(10,000\). For example, a city with an area of \(34\) ha has an area of \(34 \times 10,000 = 34,000\) square metres.
To convert an area from square metres to hectares, simply divide it by \(10,000\). For example, a block of land with an area of \(23,000\) square metres has an area of \(23,000 \div 10,000 = 2.3\) ha.
Example: Doing Conversions in Geometry Problems
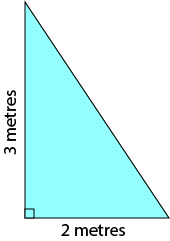
Here's a problem out of Sam's maths text book that he'd like some help with solving. He's been asked to find the area of the triangle in square millimetres.
Well Sam, the first thing you should do is find the area in square centimetres as all the measurements are given in centimetres. Remember that the area of a triangle is equal to half of its base times its height. So, the area of your triangle is \(\dfrac{1}{2} \times 2 \times 3 = 3\) square metres.
Next, multiply this area by \(1,000,000\) as each square metre is made up of \(1,000,000\) square millimetres. The answer is \(3 \times 1,000,000 = 3,000,000\) square millimetres.
Converting between Metric and Imperial Areas.
We can convert between metric and Imperial areas using similar methods. We just need to know what number to multiply each square unit by to give the conversion. Alternatively, if we know the number used to do the length conversion, we can multiply by it twice to find the number used to do the area conversion.
For example, one foot is \(0.3048\) metres. So, one square foot is equal to \(0.3048 \times 0.3048 = 0.0929\) square metres. So, to convert an area of \(100\) square feet to square metres, we simply multiply it by \(0.0929\) to give \(100 \text{ square feet} = 100 \times 0.0929 = 9.29 \text{ square metres}\).
You can convert an area in hectares into acres by multiplying it by \(2.47105\). So, an area of \(100\) acres is equal to an area of \(100 \times 2.47105 = 247.105\) acres.
As a final example, one inch is the same as \(25.4\) millimetres. So, one inch squared is the same as \(25.4 \times 25.4 = 645.16\) square millimetres. To convert an area in square inches into an area in square millimetres, simply multiply it by \(645.16\). For example, an area of \(100\) square inches is the same as an area of \(100 \times 645.16 = 64,516\) square millimetres.
You can do similar conversions between any Imperial unit of area and any metric unit of area, and vice versa. You just need to know the conversion factors (numbers to multiply by). Have fun!
Description
In these chapters, you will learn more about measurement topics such as
- Metric numbers
- Speed
- Conversions
and several other topics
Audience
Year 10 or higher, some chapters are suitable for Year 8+ students
Learning Objectives
Learn about measurement and related topics
Author: Subject Coach
Added on: 28th Sep 2018
You must be logged in as Student to ask a Question.
None just yet!