Year 10+ Measurement
Chapters
Metric (SI) Prefixes
Metric (SI) Prefixes
In the metric system, we have a number of standard units such as the second (for time), the metre (for distance), the gram (for mass), and the litre (for volume). Sometimes it isn't convenient to report measurements in these units. To cope with very large and very small numbers, the metric system includes a number of different prefixes. Prefixes are parts of a word that can be added to the beginning of another word to change its meaning. Each metric prefix refers to a different power of ten, and makes it easier to report measurements of all sizes. Let's have a look at a few examples.
Example 1
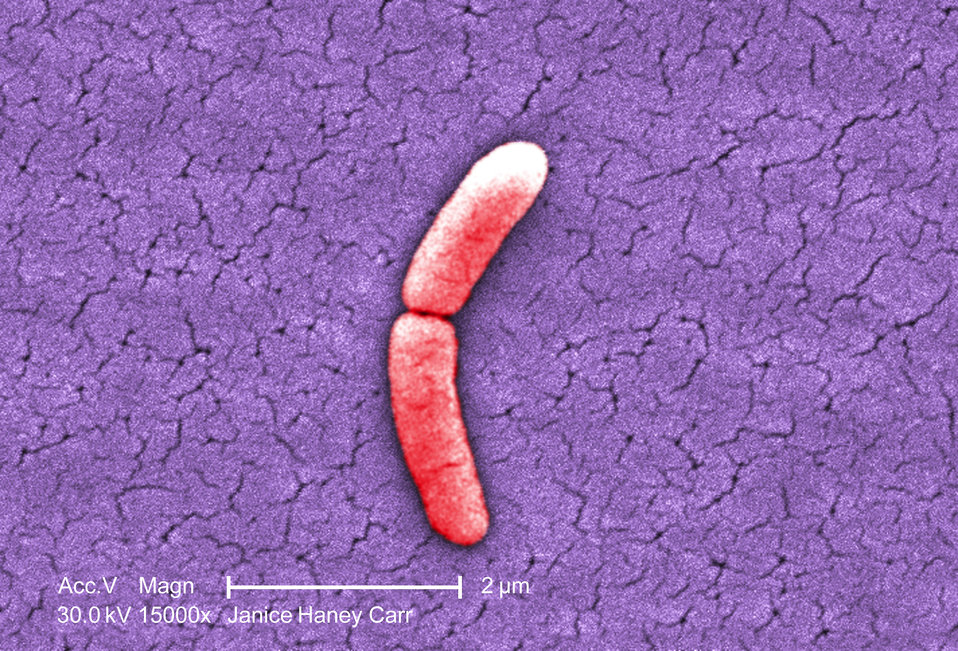
The picture on the left is a coloured electron micrograph of a Salmonella typhimurium bacterium that is undergoing cell division. You've probably heard of Salmonella: it's a nasty tummy bug that you can catch by eating contaminated food. The bacterium is impossible to see with the naked eye: this electron micrograph was taken using an electron microscope at a magnification of \(15,000 \times\). Each half of the bacterium measures \(0.000002\) m. I don't know about you, but I find it a bit tedious to have to write down all those zeroes all the time, and I can't really visualise what they mean. The metric system has found a way around this, by introducing the prefix micro, which corresponds to \(10^{-6}\). So, we could, more conveniently, write this length as \(2\) micrometres, or using the symbol \(2 \mu \text{m}\).
Example 2

If our friend the elephant got on the bathroom scales, they'd break. Using bigger scales, we can read his mass as \(3,500,000\) grams. It is much more convenient to report this mass as \(3,500\) kilograms (or kg), using the metric prefix kilo, which stands for \(10^3\).
Example 3

Sam is making a chocolate cake. He's a great cook! The recipe calls for \(5\) thousandths of a litre of vanilla essence. It makes more sense to write this as \(5\) millilitres (or \(5\) mL), using the metric prefix milli, which means \(10^{-3}\).
The Most Commonly Used Metric Prefixes
| Name | Number | Prefix | Symbol |
|---|---|---|---|
| Trillionth | \(0.000000000001\) | pico | p |
| Billionth | \(0.000000001\) | nano | n |
| Millionth | \(0.000001\) | micro | \(\mu\) |
| Thousandth | \(0.001\) | milli | m |
| Hundredth | \(0.01\) | centi | c |
| Tenth | \(0.1\) | deci | d |
| Ten | \(10\) | deka | da |
| Hundred | \(100\) | hecto | h |
| Thousand | \(1,000\) | kilo | k |
| Million | \(1,000,000\) | mega | M |
| Billion | \(1,000,000,000\) | giga | G |
| Trillion | \(1,000,000,000,000\) | tera | T |
For example, your doctor might prescribe you a dose of medicine measured in milligrams (mg) or micrograms (\(\mu\)g). My computer has \(16\) gigabytes (Gb) of memory, and its hard drive holds \(1\) terabyte (Tb) of storage. If you buy sliced meat in Norway, it is sold by the hectogram (hg), and liquids are measured in decilitres (dl).
Why don't you try writing down the names and symbols for some units yourself? For example, what is the unit for one trillionth of a gram? How about a million litres?
Prefixes for Larger and Smaller Numbers
In 1991, the list of official metric prefixes was extended up to a prefix for \(10^{24}\) (1 followed by 24 zeros) and down to a prefix for \(10^{-24}\). Here are the prefixes for these extra numbers:
| Name | Number | Prefix | Symbol |
|---|---|---|---|
| Septillionth | \(0.000 000 000 000 000 000 000 001\) | yocto | y |
| Sextillionth | \(0.000 000 000 000 000 000 001\) | zepto | z |
| Quintillionth | \(0.000 000 000 000 000 001\) | atto | a |
| Quadrillionth | \(0.000 000 000 000 001\) | femto | f |
| Quadrillion | \(1,000,000,000,000,000\) | peta | P |
| Quintillion | \(1,000,000,000,000,000,000\) | exa | E |
| Sextillion | \(1,000,000,000,000,000,000,000\) | zetta | Z |
| Septillion | \(1,000,000,000,000,000,000,000,000\) | yotta | Y |
Those are some pretty big (and pretty small) numbers! Here are some examples of their use:
- The diameter of a proton is 1.6-1.7 femtometres (fm).
- The mass of a proton is around 1.67 yoctograms (yg).
- The HIV-1 virus weighs 1 femtogram (fg).
- The mass of the Earth is 5,972.6 yottagrams (Yg), and all its oceans put together have a mass of 1.4 Yg.
- Google processed 24 petabytes (pb) of data per day in 2009.
- The Wayback machine (an archive of all the web-pages ever created since the beginning of the internet) stored 15 petabytes of data in October, 2016.
Conclusion
These are all the official prefixes used with the units of the metric system. Of course, there are many larger and smaller numbers that we can talk about, but they are not yet associated with official prefixes. That could change in the future. If you've ever played a clicker game, you may have seen some ridiculously large numbers.
I wonder what prefix we could associate with a Googol (\(10^{100}\)). Can you imagine talking about googolgrams? It's a bit of a mouthful, isn't it?
Description
In these chapters, you will learn more about measurement topics such as
- Metric numbers
- Speed
- Conversions
and several other topics
Audience
Year 10 or higher, some chapters are suitable for Year 8+ students
Learning Objectives
Learn about measurement and related topics
Author: Subject Coach
Added on: 28th Sep 2018
You must be logged in as Student to ask a Question.
None just yet!