Year 10+ 3D Geometry
Chapters
Why Are There Only Five Platonic Solids
Why Are There Only Five Platonic Solids
Platonic solids are convex solids in which every face is the same regular polygon. You'd think there might be many of them, but in fact, only five exist. Let's think about why this might be the case.
There Isn't Room At Each Vertex
The simplest explanation comes from the facts that:
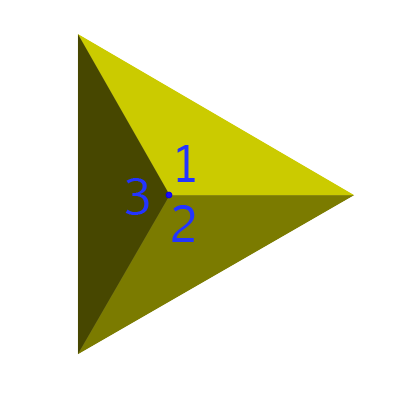
At least 3 faces have to meet at every vertex.
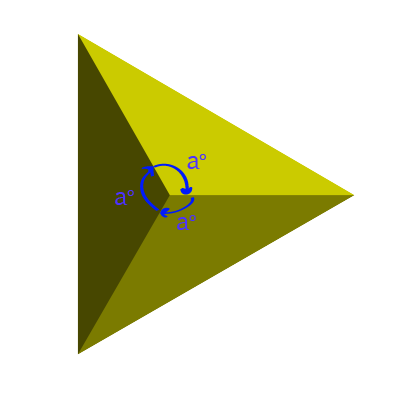
The interior angles of the faces where they meet at each vertex must add up to less than \(360^\circ\). When all the angles add up to \(360^\circ\), the vertex flattens out.
As all the faces of a Platonic Solid must be the same regular polygon, these facts limit the options.
Let's explore the possibilities:
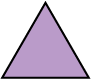
The interior angles of a regular (equilateral) triangle are \(60^\circ\). So our solid can have:
- 3 triangles meeting at each vertex (\(3 \times 60 = 180^\circ\))
- 4 triangles meeting at each vertex (\(4 \times 60 = 240^\circ\))
- 5 triangles meeting at each vertex (\(5 \times 60 = 300^\circ\))

The interior angles of a regular quadrilateral (square) are \(90^\circ\). So our solid can have:
- 3 quadrilaterals meeting at each vertex (\(3 \times 90 = 270^\circ\))

The interior angles of a regular pentagon are \(108^\circ\). So our solid can have:
- 3 pentagons meeting at each vertex (\(3 \times 108 = 324^\circ\))

The interior angles of a regular hexagon are \(120^\circ\). But \(3 \times 120 = 360^\circ\), so we can't build a solid with hexagons as it will flatten out.
We've found 5 different possibilities for the faces meeting at each vertex. So there are 5 possible different solids. Here they are:
| Faces Meeting at Each Vertex | Angle Sum at Vertex | Picture | Name of Solid |
|---|---|---|---|
| 3 Equilateral Triangles | \(180^\circ\) |  |
Tetrahedron |
| 4 Equilateral Triangles | \(240^\circ\) | 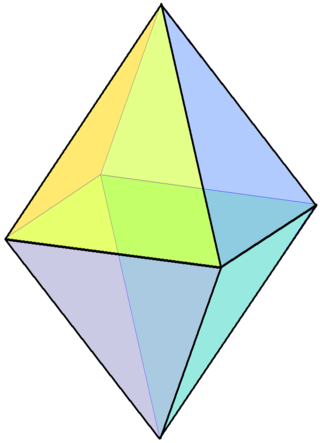 |
Octahedron |
| 5 Equilateral Triangles | \(300^\circ\) | 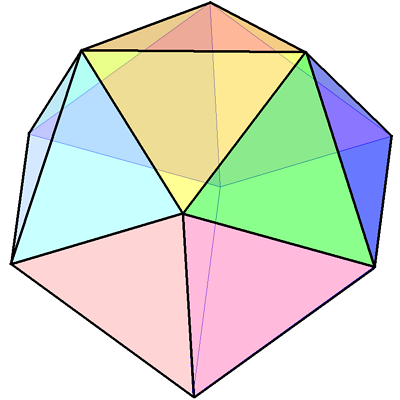 |
Icosahedron |
| 3 Squares | \(270^\circ\) | 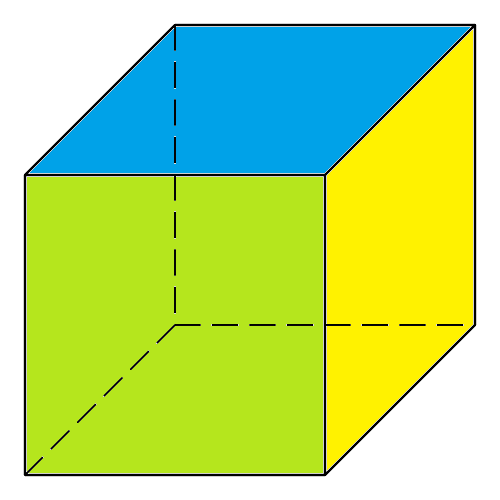 |
Cube (or Hexahedron) |
| 3 Pentagons | \(324^\circ\) | 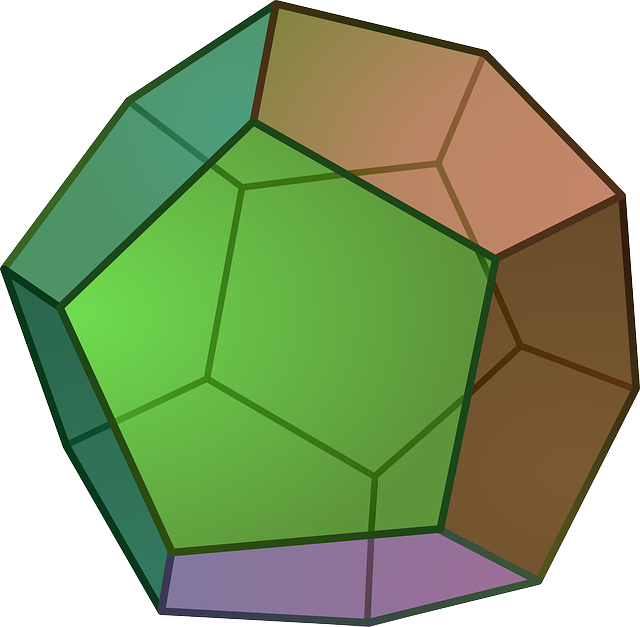 |
Dodecahedron |
An Alternative Explanation Using Euler's Formula
Euler's formula is a result that works for convex polyhedra (ones without dents). It states that the number of faces plus the number of vertices minus the number of edges must equal \(2\):
The Platonic solids are convex polyhedra, so they must satisfy Euler's formula.
Example

A tetrahedron has 4 faces, 4 vertices and 6 edges. So:
We can see why Euler's formula works by adding a vertex or an edge to a tetrahedron:
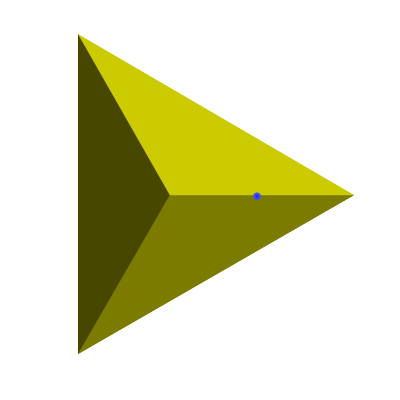
If we add an extra vertex (in the middle of one of the edges, say), then we also add an extra edge. So,

If we add an extra edge (cutting one face in half, say), then we also add an extra face. So,
No matter what we do to our solid, Euler's formula continues to give us \(2\). You can read more about Euler's formula in the article on Euler's formula.
So, How Does Euler's Formula Show Us There are Only Five Platonic Solids
Let's start with any old platonic solid. We know:
- All faces have the same number of edges. Let's call this \(n\).
- The same number of faces meet at each vertex. Let's call this \(c\). It's also equal to the number of edges that meet at each vertex.
It turns out that the numbers \(n\) and \(c\) actually are enough to tell us which Platonic solid we are dealing with.
If the number of faces in the solid is \(F\), and each face has \(n\) edges, then if we pull the solid apart so that each face lies flat, we will end up with \(nF\) edges:

Of course, in the solid, each of these edges is shared by two faces. So, if the solid has a total of \(E\) edges, we know that
Now let's deal with the vertices. When we pull our solid apart, each vertex is split into bits: one bit for each face that meets at the vertex. Let's see this happening on our tetrahedron:
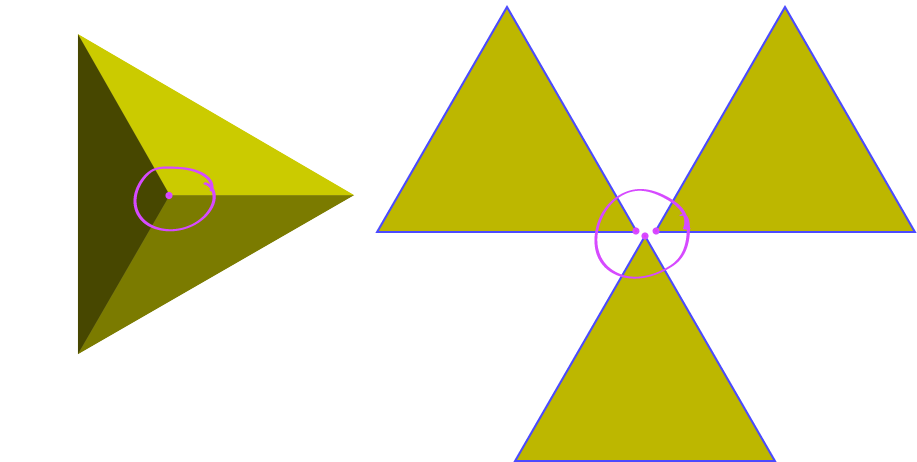
The faces of our pulled apart solid now form a collection of identical polygons, so the total number of edges is equal to the total number of vertices in the pulled apart solid. This means that
So, where does Euler's Formula Come Into It?
Let's rearrange our equations to get \(F\) and \(V\) in terms of \(E\):
Now let's see what values of \(n\) and \(c\) will work:
| n | c | \(\dfrac{1}{n} + \dfrac{1}{c}\) | \(> \dfrac{1}{2}\)? | Picture | Name of Solid |
|---|---|---|---|---|---|
| 3 | 3 | 0.66666.... | Yes |  |
Tetrahedron |
| 3 | 4 | 0.583.... | Yes |  |
Octahedron |
| 3 | 5 | 0.533.... | Yes |  |
Icosahedron |
| 4 | 3 | 0.583.... | Yes |  |
Cube (or Hexahedron) |
| 4 | 4 | 0.5 | No | No Solid | No Solid |
| 5 | 3 | 0.533.... | Yes |  |
Dodecahedron |
| 5 | 4 | 0.45 | No | No Solid | No Solid |
And nothing else will work. So, there are only five Platonic Solids.
Note: As I said earlier, the values of \(n\) and \(c\) are enough to tell you what solid you have. Together they form the Schläfli symbol for the polyhedron. Here are the Schläfli symbols for the Platonic solids:
- Tetrahedron: \(\{3,3\}\)
- Octahedron: \(\{3,4\}\)
- Icosahedron: \(\{3,5\}\)
- Cube: \(\{4,3\}\)
- Dodecahedron: \(\{5,3\}\)
Description
There are several lessons related to 3D geometry such as
- Euler's formula
- Vertices, Edges and Faces
- Volumes of 3D shapes
- etc
Even though we've titled this lesson series to be more inclined for Year 10 or higher students, however, these lessons can be read and utilized by lower grades students.
Prerequisites
Understanding of 3D shapes
Audience
Year 10 or higher, but suitable for Year 8+ students
Learning Objectives
Get to know 3D Geometry
Author: Subject Coach
Added on: 27th Sep 2018
You must be logged in as Student to ask a Question.
None just yet!