Polyhedrons

Polyhedrons are solids with flat faces. Of course, one of these solids on its own is called a polyhedron. If you want to sound clever when you're talking about two or more polyhedrons, you could call them polyhedra as this is another word for the plural of polyhedron.

Each face of a polyhedron is a polygon (a plane (flat) shape with straight edges).

Examples

Here are just a few examples of polyhedrons. Of course, there are many more.

This is a pentagonal pyramid. It has 5 faces that are triangles and one that is a pentagon.

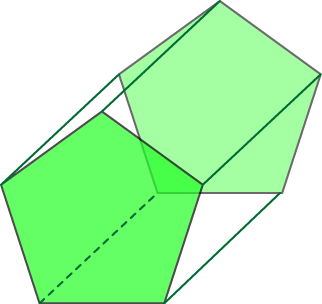
This is a hexagonal prism. It has 6 faces that are rectangles and two that are hexagons.

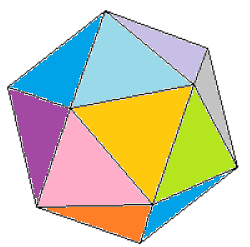
This is an icosahedron. All of its faces are triangles. How many does it have?

Some Other Common Polyhedrons

These are the Platonic solids. There are five of them. All are regular polyhedra (all faces are the same regular polygon), and they have lots of interesting properties. You can read all about them in the articles on Platonic solids.

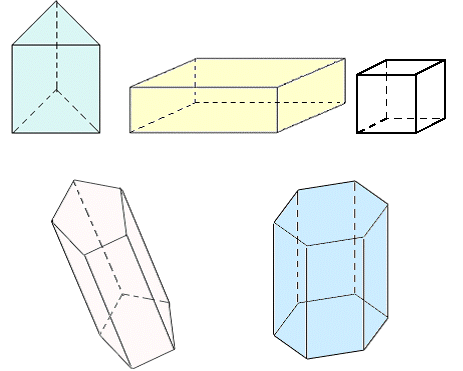
These are all prisms. They have uniform cross-sections. You can read more about prisms in the article on prisms.

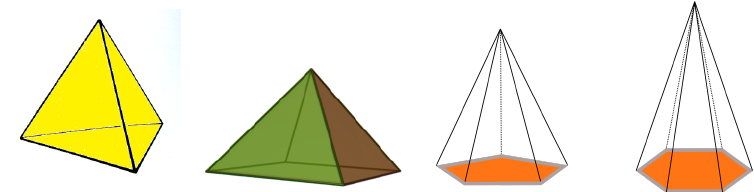
These are all pyramids. Any polygon can form the base of a pyramid. The rest of its faces are triangles. You can read more about pyramids in the article on pyramids.

There is one thing you should notice about all of these polyhedra. They have no curved surfaces. So, spheres, cones and cylinders are not polyhedra.

Origami Polyhedra

Just for a bit of fun, check out this web page on origami polyhedra. They're pretty difficult to fold, but don't they look great?

Diagonals of a Polyhedron

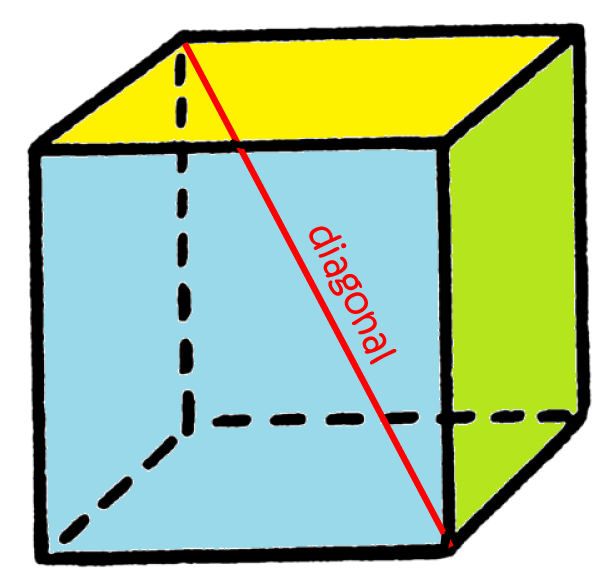
A diagonal is a line segment joining (on the inside) any two vertices of a polyhedron that are not joined by an edge. Polyhedra can have lots of different diagonals. For example, this cube has \(16\). The tetrahedron, however, has no diagonals.

Faces, Edges and Vertices

Mathematicians are interested in counting three parts of polyhedra. These are the

• Faces (the flat surfaces)
• Edges (the line segments joining each pair of faces), and the
• Vertices (the corner pointy bits)

Euler's Formula

The Swiss mathematician, Leonhard Euler, was the first to write down a formula relating the numbers of faces, edges and vertices of a convex (one without dents or holes) polyhedron. It turns out that, if we set \(V\) equal to the number of vertices, \(E\) equal to the number of edges and \(F\) equal to the number of faces of a convex polyhedron,

The above formula is called Euler's Formula.

Let's try it out on a couple of examples.

Example: Tetrahedron

The tetrahedron has

• 4 Faces
• 6 Edges
• 4 Vertices

\( V + F - E = 4 + 4 - 6 = 2\)

It works!

Example: Pentagonal Pyramid

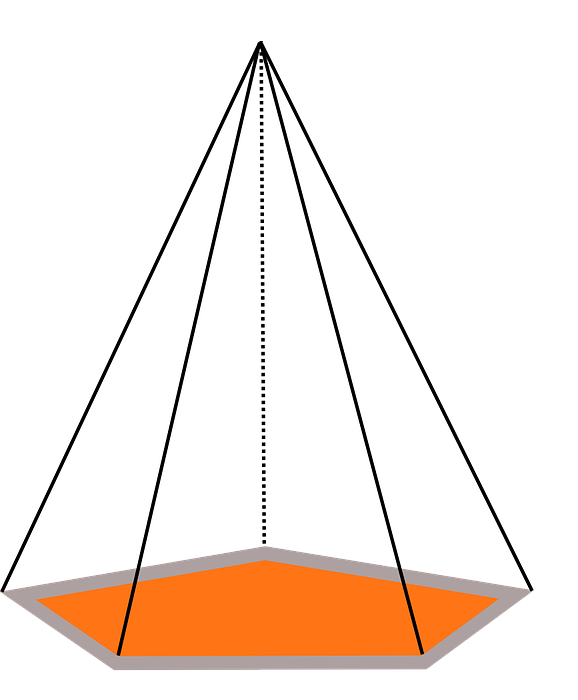
The pentagonal pyramid has

• 6 Faces
• 10 Edges
• 6 Vertices

\( V + F - E = 6 + 6 - 10 = 2\)

It worked again!

Why don't you go and try Euler's Formula out on some other polyhedra? It's useful when you are trying to write down the numbers of faces, edges and vertices and can't quite work out the number of one of them.