Year 10+ 3D Geometry
Chapters
Euler's Formula
Euler's Formula
Euler's Formula is a relationship between the numbers of faces, edges and vertices (corners) of a convex polyhedron
(a 3-D shape with flat faces and straight edges that doesn't have any dents in it).
It states that the number of vertices plus the number of faces minus the number of edges always equals \(2\).
We write Euler's Formula as

A tetrahedron is a convex polyhedron. It has \(4\) vertices, \(4\) faces and \(6\) edges. Let's test out Euler's Formula:
The Platonic Solids
Now, let's try Euler's formula on the rest of the Platonic solids.
The Cube (or Hexahedron)
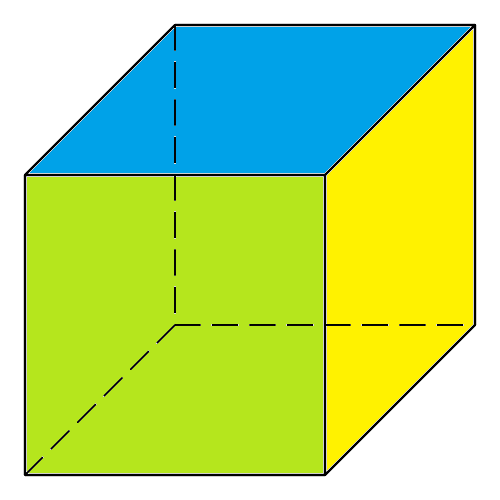
The cube has \(8\) vertices, \(6\) faces and \(12\) edges. So,
The Octahedron
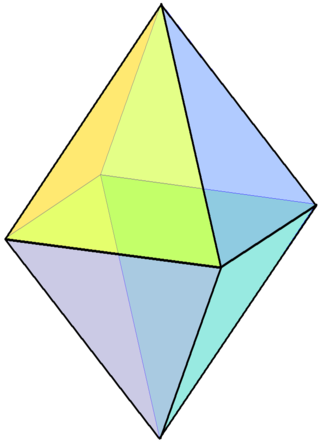
The octahedron has \(6\) vertices, \(8\) faces and \(12\) edges. So,
The Dodecahedron
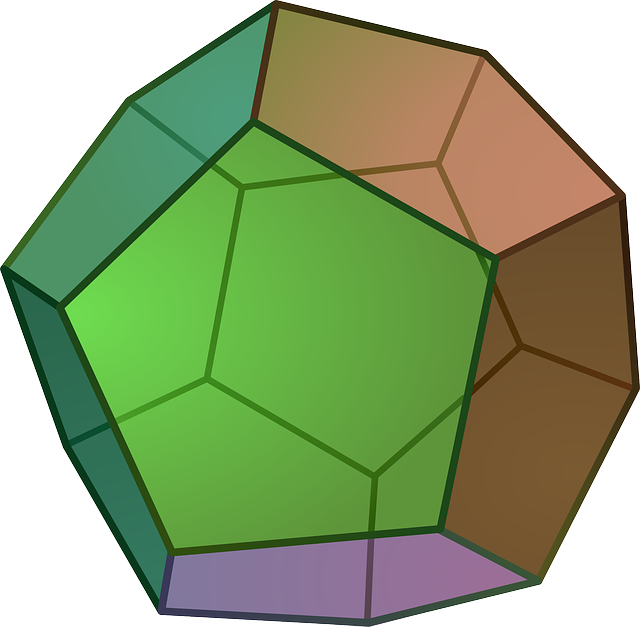
The dodecahedron has \(20\) vertices, \(12\) faces and \(30\) edges. So,
The Icosahedron
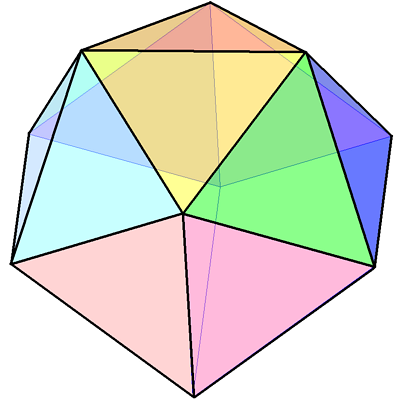
The icosahedron has \(12\) vertices, \(20\) faces and \(30\) edges. So,
Are There Solids that Euler's Formula Doesn't Work For?
Yes, Euler's formula is only guaranteed to work for convex polyhedrons. Here's a polyhedron that isn't convex. It's called a small stellated dodecahedron:

The small stellated dodecahedron (try saying that 10 times quickly) has 12 vertices, 12 faces and 30 edges. So,
Euler Characteristic
Mathematicians love to generalise things. One generalisation of Euler's formula is the Euler Characteristic. The Euler characteristic
can take on all sorts of different values (not just 2) and we can find the Euler characteristic of non-convex polyhedra and other solids that are not
polyhedra. The Euler characteristic is defined to be
Mathematicians are interested in the Euler characteristic as it doesn't change if you deform a solid: twist or bend it, squeeze it or shrink it. It is what we call a topological invariant. Let's have a look at a few examples of Euler characteristics
| Solid | Picture | \(\chi\) |
|---|---|---|
| Sphere |  |
\(2\) |
| Klein Bottle |  |
\(0\) |
| 3-holed Torus |  |
\(-4\) |
| Small Stellated Dodecahedron |  |
\(-6\) |
Note: we know that the Euler characteristic of a sphere is \(2\) because we can pump up any of the Platonic solids to form a sphere,
and their Euler characteristics are all \(2\). We say that the Platonic solids are homeomorphic to a sphere because we can deform them (by pumping
them up) to form a sphere.
Description
There are several lessons related to 3D geometry such as
- Euler's formula
- Vertices, Edges and Faces
- Volumes of 3D shapes
- etc
Even though we've titled this lesson series to be more inclined for Year 10 or higher students, however, these lessons can be read and utilized by lower grades students.
Prerequisites
Understanding of 3D shapes
Audience
Year 10 or higher, but suitable for Year 8+ students
Learning Objectives
Get to know 3D Geometry
Author: Subject Coach
Added on: 27th Sep 2018
You must be logged in as Student to ask a Question.
None just yet!