Year 10+ 3D Geometry
Chapters
Cones
Cones

Many things, like party hats and ice cream cones are shaped like cones. Wizard's hats and dunce caps are also cone-shaped. A witch's hat is shaped a bit like a cone with a brim.


We see traffic cones on our roads. They have a shape like a cone, with a bit sawn off the top and a widened-out base so that they don't topple over. We call objects
that are shaped like cones conical. So, what exactly is a cone, and what are its properties?
The Structure of a Cone
Cones are solids with a flat base, and one curved side. The flat base may be shaped like a circle or an ellipse. Most of the time, it's a circle. Cones are not polyhedrons as
they have a curved surface, and no straight edges.

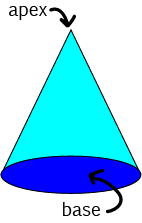
The flat bottom of a cone is called its base, and the pointy bit at the top of the cone is called its apex, as shown in the picture below.
How Do Mathematicians Build a (Circular) Cone?
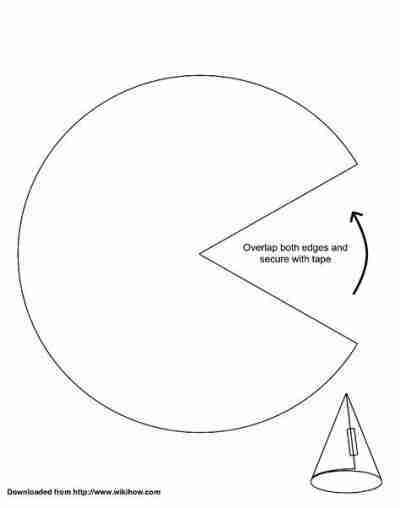
You may have made a cone yourself at some stage, by taking a bit of cardboard shaped like the one shown below and bending it around until the edges meet.
Mathematicians have a slightly more abstract view of how to create a cone. They take a right-angled triangle and rotate it around one of its two shorter sides:
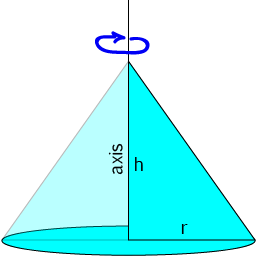
axis of the cone.
Right and Oblique Cones
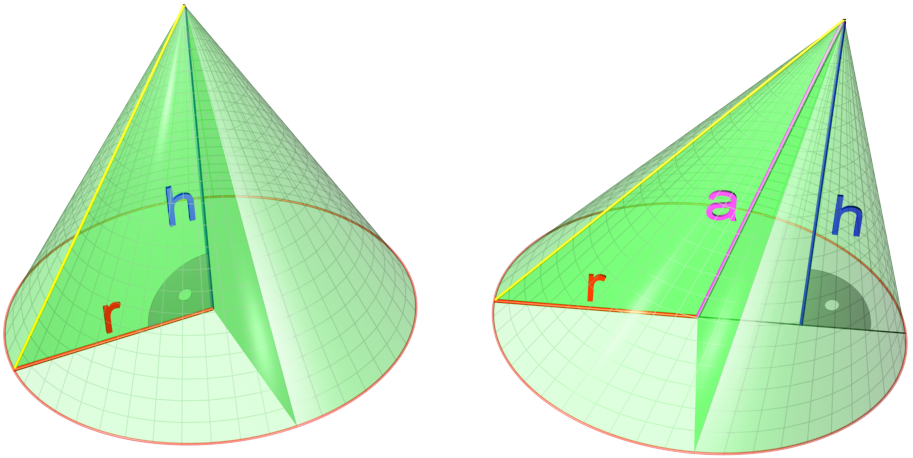
Just as with pyramids, there are two types of cones: right cones are cones in which the apex lies directly about the centre of the base, and oblique cones are cones in which it
doesn't:
Finding the Surface Area of a Cone
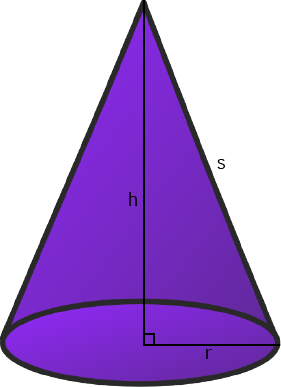
The surface area of a cone may be split up into two parts:
- The area of the base. For a circular cone, this is \(\pi r^2\), where \(r\) is the radius of the cone.
- The area of the curved surface. This is equal to \(\pi r s\), where \(r\) is the radius of the cone, and \(s\) is the slant height of the cone as shown in the picture on the left.
Note that we can use Pythagoras' theorem to find \(s = \sqrt{r^2 + h^2}\).
For example, if we were asked to find the surface area of a cone with height \(h = 3\) cm and radius \(r = 4\) cm, then we would calculate \(s = \sqrt{3^2 + 4^2} = 5\) cm, and
Finding the Volume of a Cone
The formula for the volume of a right circular cone is
For example, the volume of a cone with height \(h = 3\) cm and base radius \(r = 4\) cm is given by
Volumes of Cones and Volumes of Cylinders
Did you notice something about the formula for the volume of a cone? It looks a lot like the formula for the volume of a cylinder.
In fact, we can draw a cylinder of the same base radius and height around a cone, as shown in the picture below:
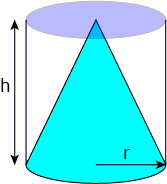
If \(\dfrac{1}{3}\) is sounding awfully familiar to you, that's because the volume of a right pyramid is also equal to \(\dfrac{1}{3}\) of the volume of the prism of the same base and height. This isn't a coincidence: you can think of a cone as a "pyramid with a circular base".
Description
There are several lessons related to 3D geometry such as
- Euler's formula
- Vertices, Edges and Faces
- Volumes of 3D shapes
- etc
Even though we've titled this lesson series to be more inclined for Year 10 or higher students, however, these lessons can be read and utilized by lower grades students.
Prerequisites
Understanding of 3D shapes
Audience
Year 10 or higher, but suitable for Year 8+ students
Learning Objectives
Get to know 3D Geometry
Author: Subject Coach
Added on: 27th Sep 2018
You must be logged in as Student to ask a Question.
None just yet!