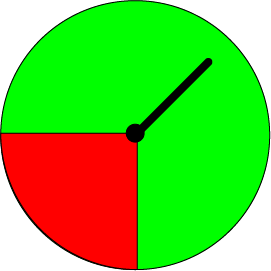
If the event is \(\{\text{Green}\}\), the complement is \(\{\text{Red}\}\).

If the event is roll an even number \(\{2,4,6\}\), the complement is rolling an odd number \(\{1,3,5\}\).

If the event is drawing a \(\{\text{Spade}\}\) from a standard deck of \(52\) playing cards, the complement is drawing one of \(\{\text{Heart, Diamond, Club}\}\).

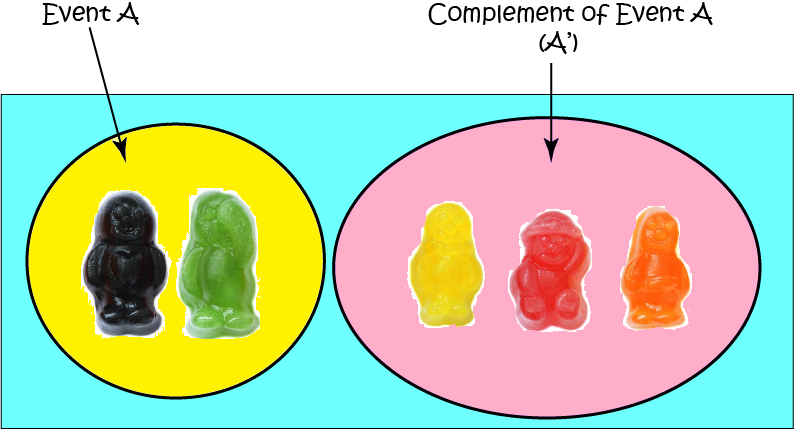
Sam's dad loves black and green jelly babies. Event \(A\) is going to denote randomly drawing a black or green jelly baby from a bag of jelly babies with equal numbers of the five different colours: green, orange, black, red and yellow. So \(A = \{\text{black}, \text{green}\}\) and \(A' = \{\text{orange}, \text{red}, \text{yellow}\}\).

The number of ways Event \(A\) can occur is \(2\), and there are a total of \(5\) possible outcomes. So, the probability of event \(A\) is:

The number of ways the complement of Event \(A\) can occur is \(3\). As the total number of outcomes is \(5\), the probability of event \(A'\) is:

Let's just check:

If you toss a coin three times, what is the probability of getting at least one head?

Solution:

There are quite a few ways that this event \(E\) can occur: \(\{HHH,HHT,HTH,THH, \dots, TTH\}\), but only one way \(\{TTT\}\) that its complement can occur. Thus, it's easier to work out the probability of the complement occurring and subtract it from one. There are a total of \(8\) possible outcomes. So, the probability of the complement is