Probability
Chapters
Independent Events
Independent Events
There is no doubt that you'll have come across a random event at some time in your life. Some examples are the outcomes of rolling a die, tossing a coin or drawing a prize from a lucky dip.
Sometimes an event affects the outcome of the next event. For example if you draw a jelly baby out of a bag and eat it, there are fewer jelly babies left in the bag. So, the next time someone draws a jelly baby out of the bag, the probabilities will be different. Events like this are called dependent events
Events where the outcome is not affected by things that have happened earlier are called independent events.
Independent Events
An event is independent if it is not affected by any event that goes before it.
Example
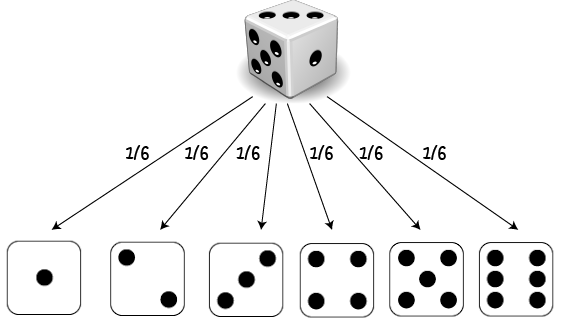
Rolling a die is an independent event.
Each roll of the die has size possible outcomes, and the result of a preceding roll does not affect the result of a current roll.
The chance of rolling a \(3\) is simply \(\dfrac{1}{6}\), regardless of how many times you have rolled the die before hand.
Each roll of the die is an independent event.
If you roll a die and it lands on "3" three times in a row, the chance of it landing on a 3 on the next roll is still \(\dfrac{1}{6}\). The previous rolls have no effect on the current roll.
Suppose you are playing a game where you need to roll a 1 or a 5 to win. You roll the die twenty times and still no 1 or 5 has appeared. Some people might think that the 1 or 5 has to turn up soon because it is "due", but this is not the case. On each roll of the die, there is still a \(\dfrac{1}{6}\) chance of getting a \(1\) and a \(\dfrac{1}{6}\) chance of getting a \(5\).
Thinking like this is called the gambler's fallacy. Of course, it is possible that the next roll could be a \(1\) or a \(5\), simply because each number is equally likely
to appear on each roll of the die.
Calculating the Probability of Independent Events
In general, the probability that an event \(E\) will happen is given by the formula:
Example

Let's go back to our die example. The number of ways of getting a \(1\) or a \(5\) is 2. The total number of outcomes is 6: 1, 2, 3, 4, 5, 6.
So, the probability of rolling a \(1\) or a \(5\) is
Expressing Probabilities
We express probabilities on a scale from
- 0 for impossible up to
- 1 for certain
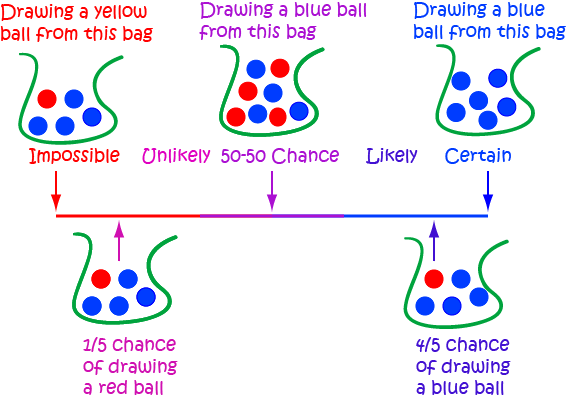
There are various ways of expressing probabilities in this range. You might use:
- A fraction e.g. \(\dfrac{1}{3}\)
- A decimal e.g. \(0.3333\dots\)
- A percentage e.g. \(33 \;\dfrac{1}{3}\%\).
- Words e.g. one in three.
Combining Two or More Indendent Events
To find the probability of two or more independent events occurring, we multiply the probabilities.
If the events are called A and B, then we write
Example 1
What is the probability of rolling a \(1\) on a 6-sided die and getting "Heads" when tossing a fair coin?
Solution:
The probability of rolling a \(1\) is \(\dfrac{1}{6}\).
The probability of getting "Heads" is \(\dfrac{1}{2}\).
These two events are independent. So, the probability of them both occurring is:
Example 2
What is the probability of getting a \(6\) three times in a row when rolling a fair die?
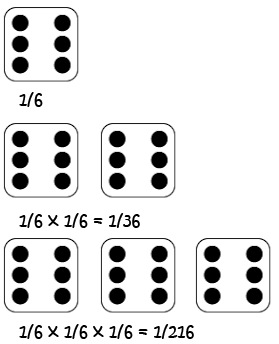
Each roll of the die is an independent event: the die has no way of reacting to what has gone before.
So, on each roll of the die, the probability of getting a \(6\) is \(P(6) = \dfrac{1}{6}\).
The probability of getting three \(6\)s in a row is \(P(6,6,6) = P(6) \times P(6) \times P(6) = \dfrac{1}{6} \times \dfrac{1}{6} \times \dfrac{1}{6} = \dfrac{1}{216}\).
Example 3: Dice Game
To win a certain dice game, you need to roll 5 of the same number with a single die in a row.
What is the probability of winning by rolling five \(6\)s in a row, starting from a given roll of the die?
Solution:
On each roll of the die, there is a \(\dfrac{1}{6}\) chance of getting a \(6\). Each roll is independent, so the probability of getting five \(6\)s in a row is
The probability of getting 5 of any given number is also \(\dfrac{1}{7776}\), but the probability of winning the game on a given set of 5 rolls is \(6 \times \dfrac{1}{7776} = \dfrac{1}{2296}\) as there are six different ways that you can get 5 of the same number.
Note: It is very unlikely to roll the same number a large number of times on a die. But, if you know that you've already rolled \(6\) one hundred times in a row, the probability of rolling a \(6\) on the 101st roll is \(\dfrac{1}{6 }\). The previous rolls of the die to not affect the next roll.
Final Example
Christo's scout group is nominating people to represent them at a regional council. Each scout has a \(\dfrac{1}{6}\) chance of being selected to proceed to the district selection round.
Once scouts have reached the district selection round, they have a \(\dfrac{1}{10}\) chance of being selected for the regional council.
What is Christo's chance of being selected for the regional council?
Solution:
To be selected for the regional council, Christo needs to complete the following two steps:
- Be selected to proceed to the district selection round: a \(\dfrac{1}{6}\) chance.
- Be selected from the district selection round to be a member of the regional council: a \(\dfrac{1}{10}\) chance.
Thus Christo's probability of selection is:
Coincidences?
Sometimes things that people say are coincidences are actually quite likely.
For example, there is about a \(70\%\) chance that two of the people in your new class (of 30 students) share the same birthday.
It turns out that for there to be a \(50\%\) or more chance that two people in a group share the same birthday (assuming that all people are equally likely to have birthdays on any day of the year) so long as there are more than 23 people in the group.
However, if you want to have a 50-50 chance that someone else in the same group shares your birthday, you need to have \(253\) people in the group. That's a bit more like a coincidence!
Summary
The probability of an event E is equal to \(\dfrac{\text{The Number of Ways E can Happen}}{\text{Total Number of Outcomes}}\).
Independent Events are events that are not affected by previous events.
To find the probability that two or more independent events occur together, we multiply the probabilities of each individual event.
Description
In this mini series, you will learn a bit more on the topic of probability, we will cover topics such as
- Ratios
- Fair dice
- Conditional probability
- Mutually exclusive events
and more
Audience
Year 10 or higher students
Learning Objectives
Explore more on the topic of probability
Author: Subject Coach
Added on: 28th Sep 2018
You must be logged in as Student to ask a Question.
None just yet!