The Fundamental Counting Principle

The Fundamental Counting Principle says that if there are

• \(a\) ways of choosing one object, and
• \(b\) ways of choosing another object,

Example 1

A restaurant has a special offer which allows you choose 1 main meal and 1 dessert from its set menu for \(\$15\). If the set menu includes 5 main meals and 3 desserts, in how many different ways can you select your meal?

The fundamental counting principle tells us that you can choose your meal in \(5 \times 3 = 15\) different ways.

Example 2

Jasmin is making vanilla cupcakes. She has 2 different types of icing and 6 different colours of sprinkles. Assuming that she decorates each cupcake with only one type of icing and only one colour of sprinkles, in how many different ways can she decorate the cupcakes?

The fundamental counting principle tells us that there are \(2 \times 6 = 12\) different icing and sprinkles combinations. This means that there are \(12\) different ways to decorate the cupcakes.

Extending the principle to more than two choices.

You just keep multiplying the numbers of ways to make each of the choices together.

Example 3

Christo is designing T-shirts for his animal appreciation club. He speaks to a T-shirt manufacturer who tells him that he has the following decisions to make.

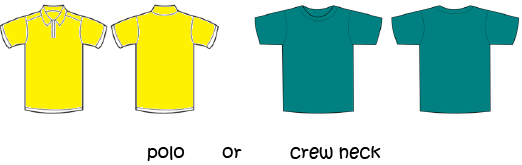
He can choose either a polo or a crew-neck shirt. So there are 2 styles to choose from.

There are 5 different colours to choose from.

Each shirt can be decorated with one of 4 different transfers.

How many different shirt designs can Christo choose from?

We can represent all this information on a tree diagram that shows all the possible choices. Unfortunately, I ran out of room for the transfers, so I've represented them using the rather cryptically chosen letters: "d" for dog, "p" for penguin, "t" for triceratops and "z" for zebra.

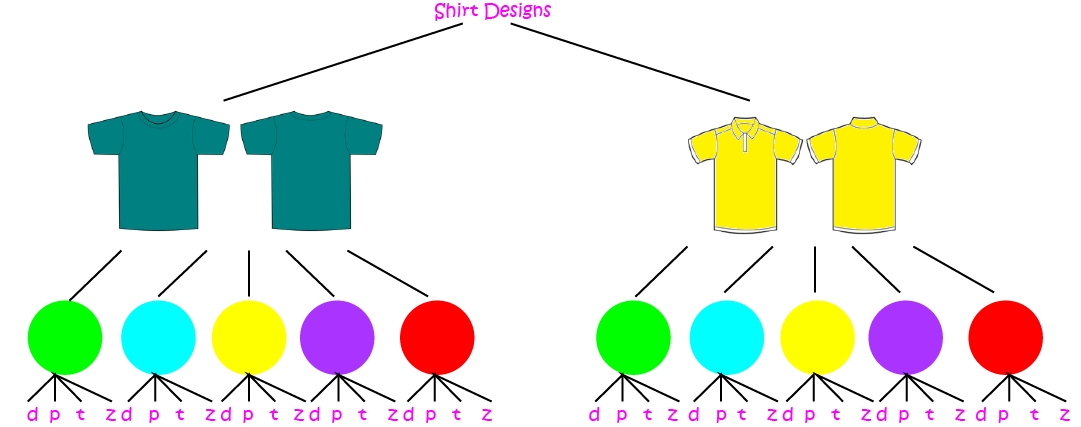
You have two options (not included in the number of T-shirt designs):

1. Count the number of options on the bottom row of the above diagram (tedious), or
2. Do a simple multiplication

I'm voting for the simple multiplication. Just multiply each number of choices together:

So Christo has to choose between \(40\) different designs. No wonder it's taking him so long!

In fact, it has taken Christo so long to make up his mind that the T-shirt manufacturer has rung him up to tell him that he no longer has purple or red polo shirts available. How many different styles can Christo choose from now?

Let's look at the new tree diagram:

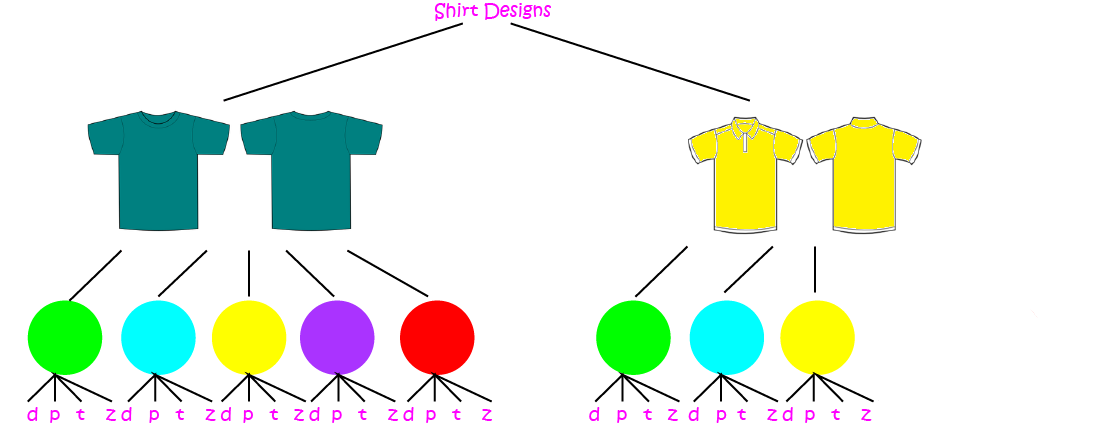
Again, there are two options:

1. Count the number of options on the bottom row of the tree diagram
2. Use the fundamental counting principle to work out how many different designs for polo shirts there are, and how many different designs for crew-neck t-shirts there are. Then add the two numbers of designs together.

Let's go with the second one:

• There are \(5 \times 4 = 20\) possible designs for crew-neck t-shirts.
• There are \(3 \times 4 = 12\) possible designs for polo shirts.

So, the total number of designs is:

You know, if Christo takes long enough making this decision, it might eventually be made for him. Maybe the T-shirt manufacturer will ring him up and tell him he only has yellow crew-neck t-shirts with zebra transfers left. I wonder if this is Christo's plan.