The Four Colour Theorem

We're going to do some colouring in. This investigation is about a very interesting mathematical result called the Four Colour Theorem.

First, here's a map of Australia. I'd like you to colour it with the smallest number of colours you need so that

• Two sections (states) that share a common border do not have the same colour.
• It's OK for states that share a common corner to have the same colour.

For the purposes of this exercise, I'd like you to forget that Bass Strait is there. We'll pretend that Tasmania and Victoria share a common border.
How many different colours do you need? Try to do it before you scroll down and look at my colouring.

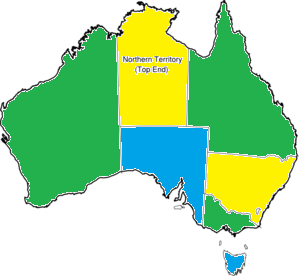
Well, I needed 3. Here's my attempt:

The Theorem

Back in the 19th Century (about 1852), mathematicians were wondering about this problem. Indeed, they wanted to know what was the smallest number of colours needed to colour in any (2-dimensional) map so that regions that shared a common boundary were coloured in different colours. Was it 3,4,5 or even 6?

It definitely wasn't 3! Here's the simplest possible map that needs 4 colours:

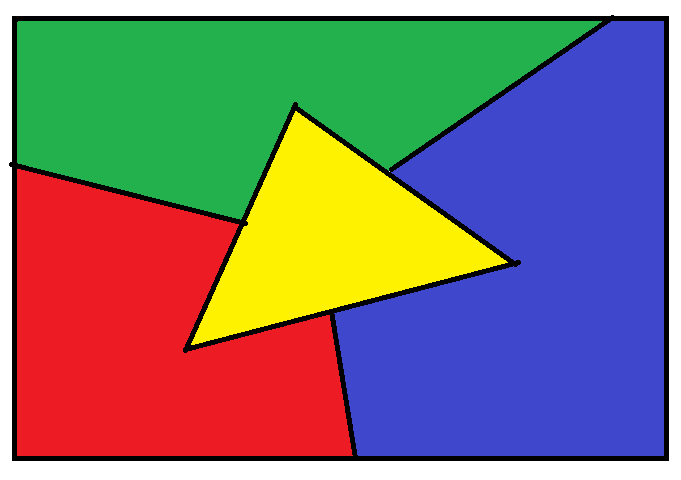
It wasn't until 1976 that the answer was finally known for sure. The minimum number of colours required to colour a map so that no two countries that shared a common border were coloured the same is 4. This result is known as the Four Colour Theorem, and it's one of the most famous theorems in mathematics.

It is partly famous (and even controversial) because it is the first major mathematical theorem that has been proved using a computer. Here's how it was done.

Kenneth Appel and Wolfgang Haaken started out by assuming that there was a map that needed more than four colours. They then proved that such a map could not have a part that resembled one of 1,936 smaller maps. Finally they showed that every map has to contain one of these 1,936 smaller maps, so the bad map could not possibly exist!

The proof required lots of calculations, and checking lots of special cases. So, Appel and Haaken wrote a computer program to do the hard work.

Many mathematicians did not like this idea, and so many doubted that the theorem was true. However, it just isn't practical to check it all by hand, so there are still people who doubt the correctness of the proof today.

In 1975, on April Fool's Day, Martin Gardner claimed that he had found a counterexample (an example showing the theorem wasn't correct) to the four colour theorem. It took 24 years to prove that this really was just an April Fool's Day joke. Why not check out Gardner's example here.

Complications Caused by Real Maps

The theorem may not work for real maps of countries like the United States that have two or more areas that are separated by other countries (like Alaska is separated from the mainland US by Canada). There's a problem if we insist that all bits of these countries are given the same colour. Here's an example where this is a problem:

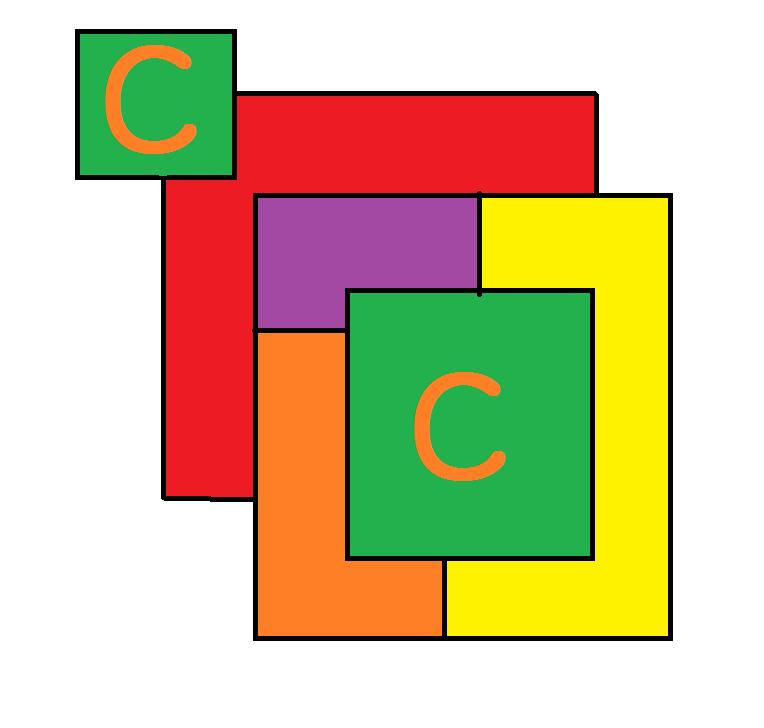
In the above example, the two regions marked with a "C" belong to the same country, and so have to be coloured in the same colour. Five colours are required to colour the map.

A hypothesis has been added to the Four Colour Theorem to exclude this possibility.

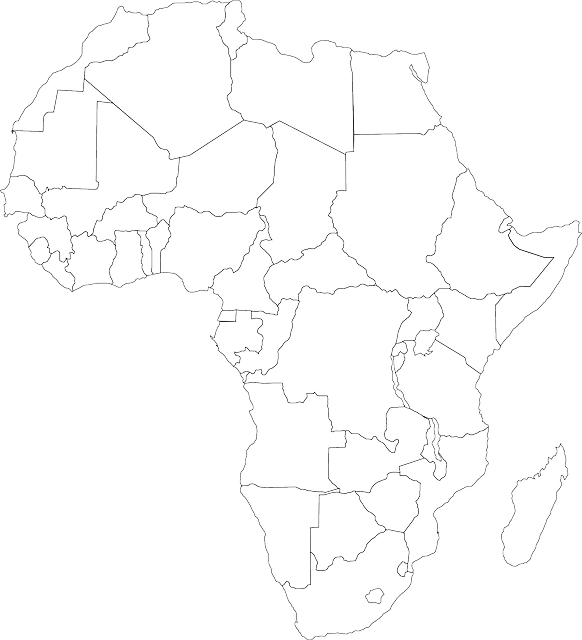
A Map For You to Colour

Why not have a go at colouring this map of Africa with only four colours. Remember: countries that share a common border need to be given different colours. Then, see if you can make a map of a fictitious country with states that needs four colours to colour it according to the rules discussed in this article. Have fun!