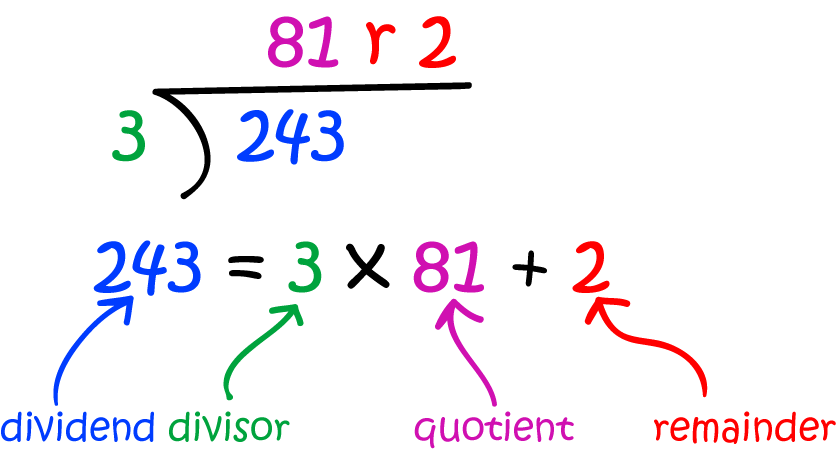
The quotient-remainder theorem is a result about arithmetic that tells us when we divide an integer \(n\) by a positive integer, \(d\), you can find unique integers \(q\) (the quotient) and \(r\) (the remainder) such that \(n = dq + r\) and \(0 \leq r

For example, when \(n = 17\) and \(d = 5\), \(17 = 5 \times 3 + 2\). So, the quotient is \(q = 3\) and the remainder is \(r = 2\).

In the example on the left, \(q = 81\) and \(r = 2\).

The quotient-remainder theorem is what makes our algorithm for long division work.