Year 10+ Mathematical Modelling
Chapters
Activity: Moving Boxes
Activity: Moving Boxes

The "Square Base" moving company is looking for a new design for their packing boxes. They want boxes with a volume of 3 cubic metres, but they want to minimise the amount of cardboard in each box. Each box must be shaped like a square prism.
They have enlisted your help for this project as they've heard wonderful things about your mathematical abilities.
Volume and Surface Area
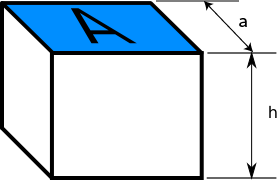
Each box must be shaped like a square prism, so we need to come up with formulas for the surface area and volume of a square prism.
For a square prism with base side-length \(a\) and height \(h\), we have:
- \(\text{Surface Area} = 2a^2 + 4ah\) and
- \(\text{Volume} = a^2h\).
Simplifying Assumptions
This project requires us to build a mathematical model for the boxes. When we build mathematical models, we employ a number of simplifying assumptions to make the calculations easier (or even possible). We can go back and make things more complicated later, but first we need to come up with something we can solve, and calculate with.
Our simplifying assumption will be that the thickness of the cardboard used to make our box does not affect its volume. So, all we need to worry about finding is the box with the smallest surface area that will hold 3 cubic metres of stuff.
Because we've been given the required volume in cubic metres, we need to work in metres. So,
- Our surface area will be measured in square metres (\(\text{m}^2\)) and
- Our volume will be measured in cubic metres (\(\text{m}^3\)).
Our required volume will be \(V = 3\). This gives us the formula:
Over to You!
Use the above formula to investigate how changing the side-length of the base affects the surface area, and find which base side-length gives the smallest surface area.
It might help to draw a graph of this function and find where there's a minimum value. You can use an on-line graphing calculator for this.
Another way to present your data would be to draw a table with headings like Base Side-Length and Surface Area for each of a range of base side-lengths like 0 m, 0.2 m, 0.4 m, 0.6 m etc.
Type up a report including your graph and table, an explanation of what you've done, and some recommendations for the company.
Modify Your Model
Once you've solved the simple problem, we need to make the model a bit more realistic.
For example, moving boxes need to have fairly thick walls. What happens to the surface area if the cardboard needs to be 0.05 m thick? How could you change your model?
Conclusion
I hope you have enjoyed this activity. It should give you an idea of the sorts of challenges and tasks that are set for professional mathematicians.
Description
In these chapters you will learn on topics of Mathematical Modelling, there is more to come under this category, these tutorials and activities are to Year 10 students or higher
Audience
Year 10 students or higher
Learning Objectives
Activities and chapters on Mathematical modelling
Author: Subject Coach
Added on: 28th Sep 2018
You must be logged in as Student to ask a Question.
None just yet!